shift2mask
Convert shift to mask vector for linear shift register
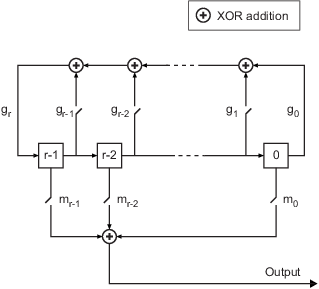
Description
mask = shift2mask(prpoly,shift)shift for a linear feedback shift register with connections specified
by the primitive polynomial prpoly.
Note
The input prpoly must be primitive to produce a meaningful
output. Use the isprimitive function to check if
prpoly is primitive. For more information, see primpoly or [2].
Examples
Input Arguments
More About
Algorithms
References
[1] Lee, J. S., and L. E. Miller, CDMA Systems Engineering Handbook, Boston, Artech House, 1998.
[2] Simon, Marvin K., Jim K. Omura, et al., Spread Spectrum Communications Handbook, New York, McGraw-Hill, 1994.
Version History
Introduced before R2006a
See Also
mask2shift | deconv | isprimitive | primpoly