nlssest
Estimate nonlinear state-space model using measured time-domain system data
Since R2022b
Syntax
Description
nssEstimated = nlssest(U,Y,nss)U and Y,
and default training options, to train the state and output networks of the idNeuralStateSpace
object nss. It returns the idNeuralStateSpace object
nssEstimated with trained state and the output networks.
nssEstimated = nlssest(Data,nss)Data, and the default
training options, to train the state and output networks of nss.
nssEstimated = nlssest(___,Options)
nssEstimated = nlssest(___,Name=Value)
Examples
This example shows how to estimate a neural-state space model with one input and one state equal to the output. First, you collect identification and validation data by simulating a linear system, then use the collected data to estimate and validate a neural state-space system, and finally compare the estimated system to the original linear system used to produce the data.
Define Linear Model for Data Collection
Define a linear time-invariant discrete-time model that can be easily simulated to collect data. For this example, use a low-pass filter with a bandwidth of about 1 rad/sec, discretized with a sample time of 0.1 sec.
Ts = 0.1; sys = ss(c2d(tf(1,[1 1]),Ts));
The identification of a neural state-space system requires you to have measurement of the system states. Therefore, transform the state-space coordinates so that the output is equal to the state.
sys.b = sys.b*sys.c; sys.c = 1;
Generate Data Set for Identification
Fix the random generator seed for reproducibility.
rng(0);
Run 1000 simulations each starting at a different initial state and lasting 1 second. Each experiment must use identical time points.
N = 1000; U = cell(N,1); Y = cell(N,1); for i=1:N % Each experiment uses random initial state and input sequence t = (0:Ts:1)'; u = 0.5*randn(size(t)); x0 = 0.5*randn(1,1); % Obtain state measurements over t x = lsim(sys,u,t,x0); % Each experiment in the data set is a timetable U{i} = array2timetable(u,RowTimes=seconds(t)); Y{i} = array2timetable(x,RowTimes=seconds(t)); end
Generate Data Set for Validation
Run one simulation to collect data that will be used to visually inspect training result during the identification progress. The validation data set can have different time points. For this example, simulate the trained model for 10 seconds.
% Use random initial state and input sequence t = (0:Ts:10)'; u = 0.5*randn(size(t)); x0 = 0.5*randn(1,1); % Obtain state measurements over t x = lsim(sys,u,t,x0); % Append the validation experiment (also a timetable) as the last entry in the data set U{end+1} = array2timetable(u,RowTimes=seconds(t)); Y{end+1} = array2timetable(x,RowTimes=seconds(t));
Create a Neural State-Space Object
Create time-invariant discrete-time neural state-space object with one state identical to the output, one input, and sample time Ts.
nss = idNeuralStateSpace(1,NumInputs=1,Ts=Ts);
Configure State Network
Define the neural network that approximates the state function as having no hidden layer (because the output layer, which is a fully connected layer, should be sufficient to approximate the linear function: ).
Use createMLPNetwork to create the network and dot notation to assign it to the StateNetwork property of nss.
nss.StateNetwork = createMLPNetwork(nss,'state', ... LayerSizes=zeros(0,1), ... WeightsInitializer="glorot", ... BiasInitializer="zeros");
Display the number of network parameters.
summary(nss.StateNetwork)
Initialized: true
Number of learnables: 3
Inputs:
1 'x[k]' 1 features
2 'u[k]' 1 features
Specify the training options for the state network. Use the Adam algorithm, specify the maximum number of epochs as 300 (an epoch is the full pass of the training algorithm over the entire training set), and let the algorithm use the entire set of 1000 experiment data as a batch set to calculate the gradient at each iteration.
opt = nssTrainingOptions('adam');
opt.MaxEpochs = 300;
opt.MiniBatchSize = N;Also specify the InputInterSample option to hold the input constant between two sampling interval. Finally, specify the learning rate.
opt.InputInterSample = "zoh";
opt.LearnRate = 0.01;Estimate the Neural State-Space System
Use nlssest to train the state network of nss, using the identification data set and the predefined set of optimization options.
nss = nlssest(U,Y,nss,opt,'UseLastExperimentForValidation',true);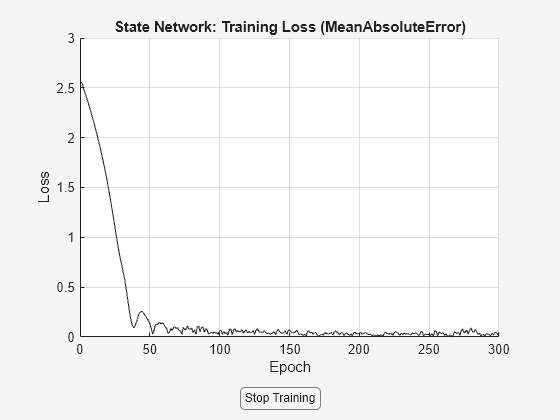
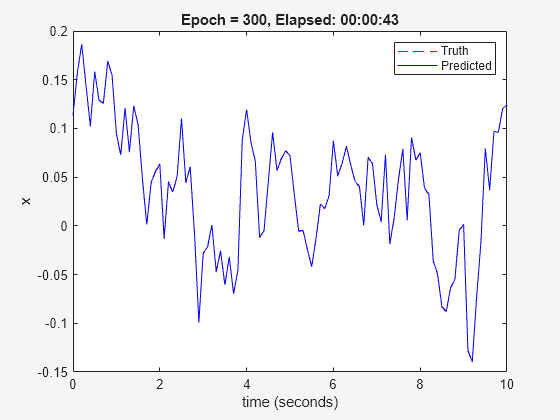
Generating estimation report...done.
The validation plot shows that the resulting system is able to reproduce well the validation data.
Compare the Estimated System to the Original Linear System
Define a random input and initial condition.
x0 = 0.3*randn(1,1); u0 = 0.3*randn(1,1);
Calculate the next state according to the linear system equation.
sys.a*x0 + sys.b*u0
ans = 0.4173
Evaluate nss at the point defined by x0 and u0.
evaluate(nss,x0,u0)
ans = 0.4176
The value of the next state calculated by evaluating nss is close to the one calculated by evaluating the linear system equation.
Display the linear system.
sys
sys =
A =
x1
x1 0.9048
B =
u1
x1 0.09516
C =
x1
y1 1
D =
u1
y1 0
Sample time: 0.1 seconds
Discrete-time state-space model.
Model Properties
Linearize nss around zero
linearize(nss,0,0)
ans =
A =
x1
x1 0.9053
B =
u1
x1 0.09488
C =
x1
y1 1
D =
u1
y1 0
Sample time: 0.1 seconds
Discrete-time state-space model.
Model Properties
The linearized system matrices are close to the ones of the original system.
Perform an Extra Validation Check
Create input time series and a random initial state.
t = (0:Ts:10)'; u = 0.5*randn(size(t)); x0 = 0.5*randn(1,1);
Simulate both the linear and neural state-space system with the same input data, from the same initial state.
% Simulate original system from x0 ylin = lsim(sys,u,t,x0); % Simulate neural state-space system from x0 simOpt = simOptions('InitialCondition',x0); yn = sim(nss,array2timetable(u,RowTimes=seconds(t)),simOpt);
Note that you can also use the following code to simulate nss.
x = zeros(size(t)); x(1)=x0; for k = 1:length(t)-1, x(k+1) = evaluate(nss,x(k),u(k)); end
Plot the outputs of both systems, also display the norm of the difference in the plot title.
stairs(t,[ylin yn.Variables]); xlabel("Time"); ylabel("State"); legend("Original","Estimated"); title(['Approximation error = ' num2str(norm(ylin-yn.Variables)) ])
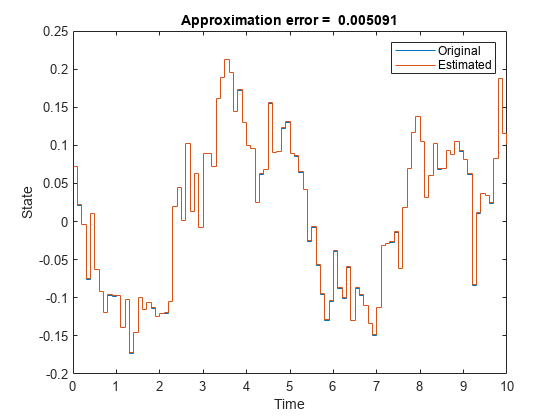
The two outputs are similar, confirming that the identified system is a good approximation of the original one.
This example shows how to estimate a nonlinear neural-state space model with no inputs and a two-dimensional continuous state equal to the output. First, you collect identification and validation data by simulating a Van der Pol system, then use the collected data to estimate and validate a neural state-space system, and finally compare the estimated system to the original system used to produce the data.
Define Model for Data Collection
Define a time-invariant continuous-time autonomous model that can be easily simulated to collect data. For this example, use an unforced Van der Pol oscillator (VDP) system, which is an oscillator with nonlinear damping that exhibits a limit cycle.
Specify the state equation using an anonymous function, using a damping coefficient of 1.
dx = @(x) [x(2); 1*(1-x(1)^2)*x(2)-x(1)];
Generate Data Set for Identification
Fix the random generator seed for reproducibility.
rng(0);
Run 1000 simulations each starting at a different initial state and lasting 2 seconds. Each experiment must use identical time points.
N = 1000; t = (0:0.1:2)'; Y = cell(1,N); for i=1:N % Create random initial state within [-2,2] x0 = 4*rand(2,1)-2; % Obtain state measurements over t (solve using ode45) [~, x] = ode45(@(t,x) dx(x),t,x0); % Each experiment in the data set is a timetable Y{i} = array2timetable(x,RowTimes=seconds(t)); end
Generate Data Set for Validation
Run one simulation to collect data that will be used to visually inspect training result during the identification progress. The validation data set can have different time points. For this example, use the trained model to predict VDP behavior for 10 seconds.
% Create random initial state within [-2,2] t = (0:0.1:10)'; x0 = 4*rand(2,1)-2; % Obtain state measurements over t (solve using ode45) [~, x] = ode45(@(t,x) dx(x),t,x0); % Append the validation experiment (also a timetable) as the last entry in the data set Y{end+1} = array2timetable(x,RowTimes=seconds(t));
Create a Neural State-Space Object
Create time-invariant continuous-time neural state-space object with a two-element state vector identical to the output, and no input.
nss = idNeuralStateSpace(2);
Configure State Network
Define the neural network that approximates the state function as having two hidden layers with 12 neurons each, and hyperbolic tangent activation function.
Use createMLPNetwork to create the network and dot notation to assign it to the StateNetwork property of nss.
nss.StateNetwork = createMLPNetwork(nss,'state', ... LayerSizes=[12 12], ... Activations="tanh", ... WeightsInitializer="glorot", ... BiasInitializer="zeros");
Display the number of network parameters.
summary(nss.StateNetwork)
Initialized: true
Number of learnables: 218
Inputs:
1 'x' 2 features
Specify the training options for the state network. Use the Adam algorithm, specify the maximum number of epochs as 400 (an epoch is the full pass of the training algorithm over the entire training set), and let the algorithm use the entire set of 1000 experiments as a batch set to calculate the gradient at each iteration.
opt = nssTrainingOptions('adam');
opt.MaxEpochs = 400;
opt.MiniBatchSize = N;Also specify the learning rate.
opt.LearnRate = 0.005;
Estimate the Neural State-Space System
Use nlssest to train the state network of nss, using the identification data set and the predefined set of optimization options.
nss = nlssest([],Y,nss,opt,'UseLastExperimentForValidation',true);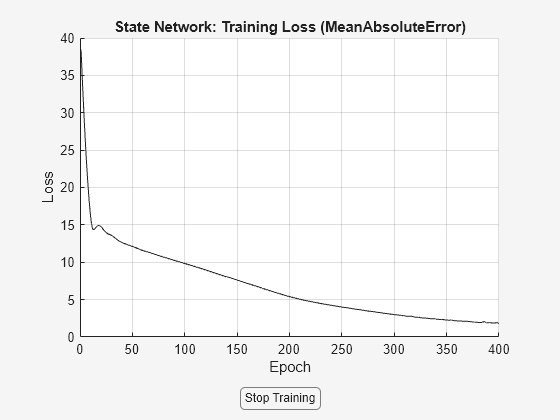

Generating estimation report...done.
The validation plot shows that the resulting system is able to reproduce well the validation data.
Compare the Estimated System to the Original Linear System
Define a random initial condition.
x0 = 0.3*randn(2,1);
Calculate the state derivative according to the original system equation.
dx(x0)
ans = 2×1
0.3111
0.3243
Evaluate nss at x0.
evaluate(nss,x0)
ans = 2×1
0.3212
0.3202
The value of the state derivative calculated by evaluating nss is close to the one calculated by evaluating the original system equation.
You can linearize nss around an operating point, and apply linear control analysis and synthesis methods on the resulting linear time-invariant state-space system.
sys = linearize(nss,x0)
sys =
A =
x1 x2
x1 0.02938 1.128
x2 -0.9763 1.045
B =
Empty matrix: 2-by-0
C =
x1 x2
y1 1 0
y2 0 1
D =
Empty matrix: 2-by-0
Continuous-time state-space model.
Model Properties
Simulate the Neural State-Space System
Create a time sequence and a random initial state.
t = (0:0.1:10)'; x0 = 0.3*randn(2,1);
Simulate both the original and neural state-space system with the same input data, from the same initial state.
% Simulate original system from x0 [~, x] = ode45(@(t,x) dx(x),t,x0); % Simulate neural state-space system from x0 simOpt = simOptions('InitialCondition',x0,'OutputTimes',t); xn = sim(nss,zeros(length(t),0),simOpt);
Plot the outputs of both systems, also display the norm of the difference in the plot title.
figure; subplot(2,1,1) plot(t,x(:,1),t,xn(:,1)); ylabel("States(1)"); legend("Original","Estimated"); title(['Approximation error = ' num2str(norm(x-xn)) ]) subplot(2,1,2) plot(t,x(:,2),t,xn(:,2)); xlabel("Time"); ylabel("States(2)"); legend("Original","Estimated");

The two outputs are similar, confirming that the identified system is a good approximation of the original one.
Input Arguments
Input data. Specify U as:
A timetable containing a variable for each input. The variable names of the timetable must match the input names of
nss, and its row times must bedurationobjects. This timetable represents a single experiment. For more information, seetimetableandduration.A double matrix with one column for each input signal and one row for each time step. Use this option only if the system is discrete-time (that is
nss.Tsis greater than zero). This matrix represents a single experiment.A cell array of N experiments composed of timetables or double matrices. All the experiments must contain the same time points. In other words the time vector corresponding to all the observations must match.
An empty array,
[], ifnsshas no inputs (that issize(nss,2)is zero).
Output data. Specify Y as:
A timetable containing a variable for each output. The variable names of the timetable must match the output names of
nss, and its row times must bedurationobjects. This timetable represents a single experiment. For more information, seetimetableandduration.A double matrix with one column for each output signal and one row for each time step. Use this option only if the system is discrete-time (that is
nss.Tsis greater than zero). This matrix represents a single experiment.A cell array of N experiments composed of timetables or double matrices. All the experiments must contain the same time points. In other words the time vector corresponding to all the observations must match.
Note
The first nx channels in
Y must be state measurements (here,
nx is the number of states specified in
nss).
Input and output data, specified as a timetable or iddata object. This argument allows you to specify the training data using a
single input argument rather than separate U and
Y arguments. Specify Data as one of the following:
An
iddataobject. If you have multiple experiments, create a multi-experimentiddataobject. Use this option if all the input and output variables in an experiment share the time vector. For more information, seemerge (iddata).A timetable. The timetable must contain a variable for each of the input and output variables in
nss. In the multi-experiment case, use a cell array of timetables. All the timetables in the cell array must use the same time vector.
Neural state-space system, specified as an idNeuralStateSpace object.
Training options, specified as an nssTrainingADAM, nssTrainingSGDM, nssTrainingRMSProp, or nssTrainingLBFGS object. Create the training options set object options
using the nssTrainingOptions command. If nss contains a
non-state output network (that is, if nss.OutputNetwork contains two
networks), you can pick different training options for the state transition function
network, nss.StateNetwork, and the nontrivial output function
nss.OutputNetwork(2). Note that
nss.OutputNetwork(1) does not contain any learnable parameters
because it is always fixed to the identity function returning all the states as
outputs.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: UseLastExperimentForValidation = true
Option to use the last experiment for validation, specified as one of the following:
true— The last experiment is not used for training, but only to display a validation plot after a number of epochs specified byValidationFrequency. This allows you to monitor the estimation performance during the training process. The last experiment can have a different duration than all the other experimentsfalse— All experiments are used for training, and no validation plot is displayed.
Validation frequency, specified as a positive integer. This is the number of epochs after which the validation plot is updated with a new comparison (new predicted output against measured outputs).
Output Arguments
Estimated neural state-space system, returned as an idNeuralStateSpace object.
Version History
Introduced in R2022b
See Also
Objects
idNeuralStateSpace|nssTrainingADAM|nssTrainingSGDM|nssTrainingRMSProp|nssTrainingLBFGS|idss|idnlgrey
Functions
createMLPNetwork|setNetwork|nssTrainingOptions|generateMATLABFunction|idNeuralStateSpace/evaluate|idNeuralStateSpace/linearize|sim
Blocks
Live Editor Tasks
Topics
- What Are Neural State-Space Models?
- Estimate Neural State-Space System
- Estimate Nonlinear Autonomous Neural State-Space System
- Neural State-Space Model of Simple Pendulum System
- Reduced Order Modeling of a Nonlinear Dynamical System Using Neural State-Space Model with Autoencoder
- Augment Known Linear Model with Flexible Nonlinear Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)