Linear Algebra
Linear algebra functions in MATLAB® provide fast, numerically robust matrix calculations. Capabilities include a variety of matrix factorizations, linear equation solving, computation of eigenvalues or singular values, and more. For an introduction, see Matrices in the MATLAB Environment.
Functions
Topics
- Matrices in the MATLAB Environment
Matrix creation and basic operations.
- Systems of Linear Equations
Solve several types of systems of linear equations.
- Eigenvalues
Eigenvalue and eigenvector computation.
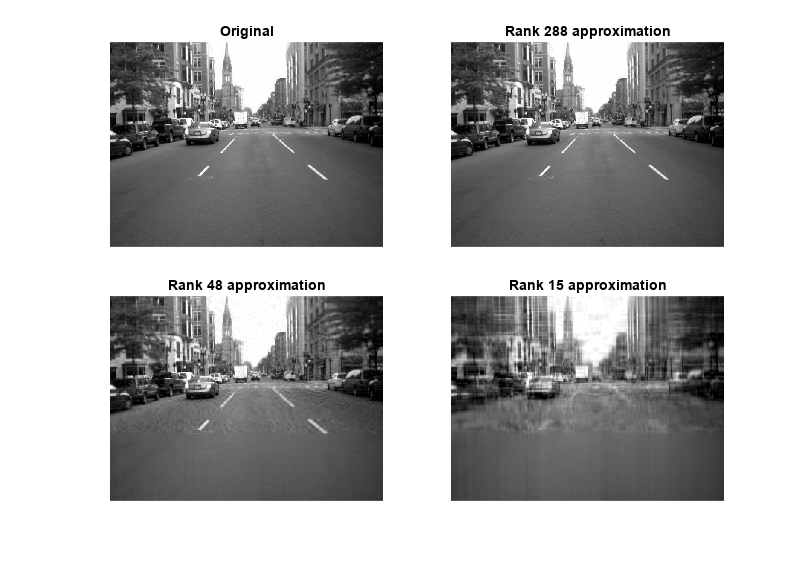
- Singular Values
Singular value decomposition (SVD).
- Factorizations
Common matrix factorizations (Cholesky, LU, QR).
- Matrix Exponentials
This example shows three of the 19 ways to compute the exponential of a matrix.
- Determine Whether Matrix Is Symmetric Positive Definite
This topic explains how to use the
cholandeigfunctions to determine whether a matrix is symmetric positive definite (a symmetric matrix with all positive eigenvalues). - LAPACK in MATLAB
LAPACK provides a foundation of routines for linear algebra functions and matrix computations in MATLAB.