idualtree2
Kingsbury Q-shift 2-D inverse dual-tree complex wavelet transform
Description
imrec = idualtree2(A,D)A, and cell array of wavelet coefficients,
D. A and D are outputs of
dualtree2.
For
the reconstruction, idualtree2 uses two sets of filters:
Orthogonal Q-shift filter of length 10
Near-symmetric biorthogonal filter pair with lengths 7 (scaling synthesis filter) and 5 (wavelet synthesis filter)
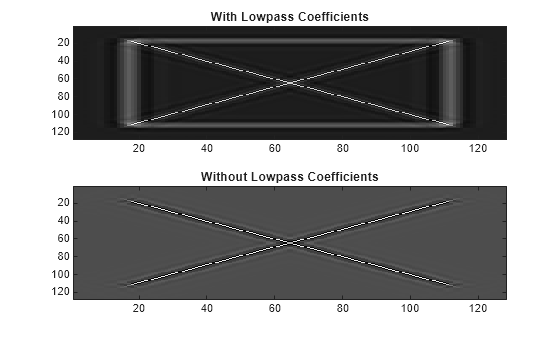
imrec = idualtree2(___,Name,Value)'LowpassGain',0.1 applies a gain of 0.1 to the final-level
approximation coefficients.
Examples
Input Arguments
Name-Value Arguments
References
[1] Antonini, M., M. Barlaud, P. Mathieu, and I. Daubechies. “Image Coding Using Wavelet Transform.” IEEE Transactions on Image Processing 1, no. 2 (April 1992): 205–20. https://doi.org/10.1109/83.136597.
[2] Kingsbury, Nick. “Complex Wavelets for Shift Invariant Analysis and Filtering of Signals.” Applied and Computational Harmonic Analysis 10, no. 3 (May 2001): 234–53. https://doi.org/10.1006/acha.2000.0343.
[3] Le Gall, D., and A. Tabatabai. “Sub-Band Coding of Digital Images Using Symmetric Short Kernel Filters and Arithmetic Coding Techniques.” In ICASSP-88., International Conference on Acoustics, Speech, and Signal Processing, 761–64. New York, NY, USA: IEEE, 1988. https://doi.org/10.1109/ICASSP.1988.196696.
Extended Capabilities
Version History
Introduced in R2020a