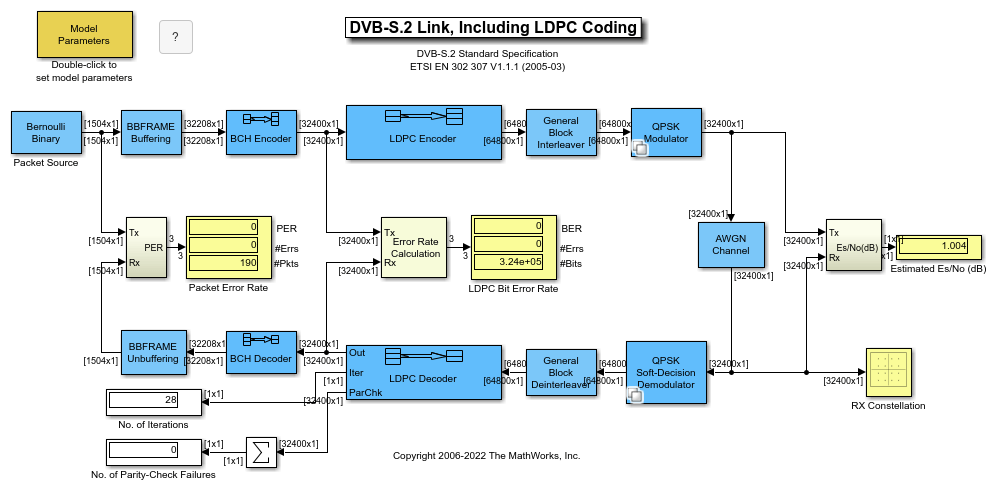
BCH Decoder
Decode BCH code to recover binary vector data
Libraries:
Communications Toolbox /
Error Detection and Correction /
Block
Description
The BCH Decoder block recovers a binary message vector from a binary BCH codeword vector. For proper decoding, the Codeword length, N and Message length, K parameter values in this block must match the parameters in the corresponding BCH Encoder block. The full-length values of N and K must produce a valid narrow-sense BCH code.
If the encoder is processing multiple codewords per frame, then the same puncture pattern holds for all codewords. The input and output signal lengths are listed in Input and Output Signal Length in BCH Blocks.
See Tips for information about valid N values, valid (N,K) pairs, and error-correcting capabilities for a given BCH code.
If decoding fails, the message portion of the decoder input is returned unchanged as the decoder output.
The sample times of all input and output signals are equal.
This icon shows optional ports.![]()
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
Tips
To generate the list of valid (
N,K) pairs along with the corresponding values of the error-correction capability, runbchnumerr(N).Valid values for
N= 2M–1, where M is an integer from 3 through 16. The maximum allowable value ofNis 65,535.
Algorithms
This block implements the algorithm, inputs, and outputs described in Algorithms for BCH and RS Errors-only Decoding.
References
[1] Wicker, Stephen B. Error Control Systems for Digital Communication and Storage. Upper Saddle River, NJ: Prentice Hall, 1995.
[2] Berlekamp, Elwyn R. Algebraic Coding Theory. New York: McGraw-Hill, 1968.
[3] Clark, George C., Jr., and J. Bibb Cain. Error-Correction Coding for Digital Communications. New York: Plenum Press, 1981.
Extended Capabilities
Version History
Introduced before R2006a