Quantization of Deep Neural Networks
Most pretrained neural networks and neural networks trained using Deep Learning Toolbox™ use single-precision floating point data types. As such, even small trained neural networks require a considerable amount of memory and hardware that can perform floating-point arithmetic. These restrictions can inhibit deployment of deep learning capabilities to low-power microcontrollers and FPGAs.
You can use the Deep Learning Toolbox Model Compression Library to quantize a network to use 8-bit scaled integer data types. Converting to integer data types reduces the memory of parameters in your network and facilitates deploying your network to hardware that performs fixed-point arithmetic.
The Deep Learning Toolbox Model Compression Library support package also facilitates structural compression techniques like projection and pruning of deep neural networks to reduce their memory requirements. Structural compression reduces the memory of a neural network by reducing the total number of parameters. For more information about other model compression techniques, see Reduce Memory Footprint of Deep Neural Networks.
Benefits of Quantization
When deploying deep learning models to hardware, especially those with data type and memory constraints, quantization improves network performance by reducing peak activation energy of the network by up to a factor of four. Network accuracy is largely maintained despite the conversion to lower-precision data types.
To learn more about the scaling, precision, and ranges of the 8-bit scaled integer data types used in the Deep Learning Toolbox Model Compression Library support package, see Data Types and Scaling for Quantization of Deep Neural Networks.
Quantization Workflow Overview
The pre-deployment quantization workflow is similar for all intended deployment hardware: create and prepare a quantization object, calibrate, quantize, and validate. You can complete these steps at the command line or in the Deep Network Quantizer app. Both options follow the same steps, but the app provides additional visualization of the data types.
Before starting the quantization workflow, consider using the structural compression techniques of pruning and projection. For more information on compression techniques in the Deep Learning Toolbox Model Compression Library, see Reduce Memory Footprint of Deep Neural Networks.
For information about maximum possible memory reduction and layer support for pruning, projection, and quantization for your network, analyze your network for compression in the Deep Network Designer app.
Create and Prepare Quantization Object
To start the quantization workflow, create a dlquantizer object with your deep neural network. Select the
execution environment that corresponds to your deployment hardware.
For microcontrollers or CPUs, such as the ARM® Cortex®-M or ARM Cortex-A, select
"MATLAB".For NVIDIA® GPUs, select
"GPU".For Intel® or Xilinx® FPGA boards, select
"FPGA".
Prepare your network before calibration using the prepareNetwork function. Network preparation modifies your neural
network to improve performance and avoid error conditions in the quantization
workflow.
In the Deep Network Quantizer app, create a dlquantizer object by
clicking New and selecting Quantize a
Network. To prepare the network, select Prepare network
for quantization.
Calibrate
To collect the dynamic ranges of the learnable parameters of your network,
calibrate the dlquantizer object using the calibrate function. Calibration helps determine data types that will
cover the range, avoid overflow, and allow underflow since scaled 8-bit integer data
types have limited precision and range when compared to single-precision floating
point data types. For the best quantization results, the calibration data must be
representative of inputs to the network.
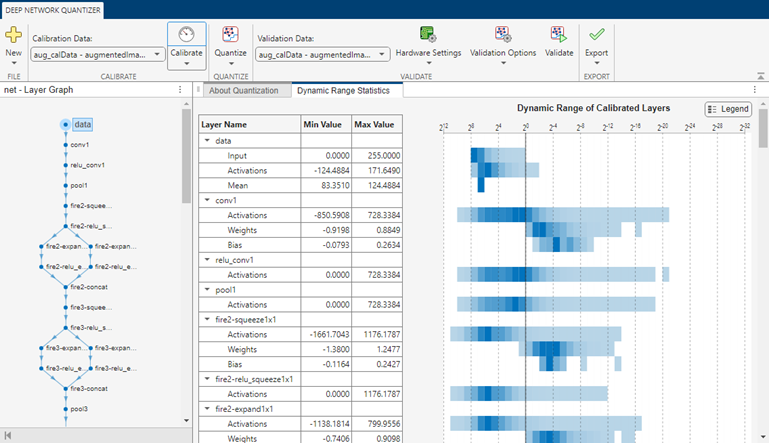
In the Deep Network Quantizer app, select your calibration data, then click Calibrate. When the calibration is complete, the app displays a table of the minimum and maximum values of the learnable parameters of the network. To the right of the table, the app displays histograms of the dynamic ranges of the parameters. To learn more about the histograms, see Data Types and Scaling for Quantization of Deep Neural Networks.
Quantize
Quantize the dlquantizer object using the quantize function. This action produces a simulatable quantized
network.
In the Deep Network Quantizer app, click Quantize. When quantization is complete, the histograms of the dynamic ranges update to show the data that can be represented with quantized representation. Data that cannot be represented is indicated with a gray region.

Validate
To determine the accuracy of your quantized network, validate the
dlquantizer object using the validate function. The validate function
determines the default metric function to use for the validation based on the type
of network that is being quantized. The DAGNetwork and SeriesNetwork objects have several default metric functions you can
use, or you can write your own custom metric function. For an example with a custom
metric function for a dlnetwork object, see Quantize Multiple-Input Network Using Image and Feature Data.
In the Deep Network Quantizer app, select a validation scheme and click Validate.
Quantization for Microcontroller Deployment
For deploying quantized networks to a microcontroller or CPU, the generated code is library-free C/C++, which allows flexibility in hardware choices. However, ARM Cortex-M or ARM Cortex-A are the recommended hardware.
To deploy a quantized network to a microcontroller or CPU:
Follow the pre-deployment workflow steps in Quantization Workflow Overview, with the execution environment set to
"MATLAB"when you create thedlquantizerobject.Export the quantized network to Simulink® using the
exportNetworkToSimulinkfunction.Generate plain C/C++ code for the generated Simulink model using Embedded Coder® or Simulink Coder™.
For an example of quantization for microcontroller deployment, see Export Quantized Networks to Simulink and Generate Code.
Quantization for GPU Deployment
For deploying quantized networks to a GPU, the Deep Learning Toolbox Model Compression Library supports NVIDIA GPUs. For more information on supported hardware, see GPU Coder Supported Hardware (GPU Coder).
To deploy a quantized network to a GPU:
Follow the pre-deployment workflow steps in Quantization Workflow Overview, with the execution environment set to
"GPU"when you create thedlquantizerobject.Provide the calibration results file from the
calibratefunction to thecodegen(MATLAB Coder) command.
For more information on generating code for GPU deployment, see Generate INT8 Code for Deep Learning Networks (GPU Coder).
For an example of quantization for GPU deployment, see Quantize Semantic Segmentation Network and Generate CUDA Code.
Quantization for FPGA Deployment
For deploying quantized networks to an FPGA board, the Deep Learning Toolbox Model Compression Library supports Intel and Xilinx FPGA boards. For more information on supported hardware, see Deep Learning HDL Toolbox Supported Hardware (Deep Learning HDL Toolbox).
To deploy a quantized network to an FPGA board:
Follow the pre-deployment workflow steps in Quantization Workflow Overview, with the execution environment set to
"FPGA"when you create thedlquantizerobject.Provide the calibrated
dlquantizerobject to thedlhdl.Workflow(Deep Learning HDL Toolbox) class.
For more information on generating code for FPGA deployment, see Code Generation and Deployment (Deep Learning HDL Toolbox).
For an example of quantization for FPGA deployment, see Classify Images on FPGA by Using Quantized GoogLeNet Network (Deep Learning HDL Toolbox).
Other Considerations for Quantization
Prerequisites
To learn about the products required to quantize and deploy a deep learning network, see Quantization Workflow Prerequisites.
For information on the layers and networks supported for quantization, see Supported Layers for Quantization.
To learn how to prepare your data set for the quantization workflow, see Prepare Data for Quantizing Networks.
Additional Tools
These tools can help you throughout the quantization workflow.
Analyze for compression in the Deep Network Designer app for information about maximum possible memory reduction and layer support for projection, pruning, and quantization of your network.
Estimate network metrics for neural network layers with the
estimateNetworkMetricsfunction.Equalize layer parameters with the
equalizeLayersfunction. Note that theprepareNetworkfunction equalizes layer parameters using the same method asequalizeLayers.
Additional Compression Methods
Quantization is one of three compression methods in the Deep Learning Toolbox Model Compression Library. For greater overall compression of your model, consider pruning and projecting in addition to quantization. To learn more about model compression techniques, see Reduce Memory Footprint of Deep Neural Networks. For an example that combines pruning, projection, and quantization, see Train and Compress AI Model for Road Damage Detection.
CPU Execution Environment
The "CPU" execution environment is available for the
quantization workflow. You can use the CPU execution environment to generate code
dependent on the ARM Compute Library, but the execution environment has limited supported
layers and supported methods. The "MATLAB" execution environment
is recommended for use to deploy to CPU devices.
For more information on using the CPU execution environment, see Generate int8 Code for Deep Learning Networks (MATLAB Coder). For an example of quantization for deployment to a Raspberry Pi® using the CPU execution environment, see Generate INT8 Code for Deep Learning Network on Raspberry Pi (MATLAB Coder).