dsp.SpectrumAnalyzer
(To be removed) Display frequency spectrum of time-domain signals
The
dsp.SpectrumAnalyzerobject will be removed in a future release. Use thespectrumAnalyzerMATLAB® object instead.The
CCDFMeasurementsproperty of thedsp.SpectrumAnalyzerobject will be removed in a future release. Use thepowermeterobject instead to compute and visualize CCDF measurements.
For more information on how to replace your existing code, see Version History.
Description
The Spectrum Analyzer System object™ displays the frequency spectrum of time-domain signals. This scope supports variable-size input, which allows the input frame size to change. Frame size is the first dimension of the input vector. The number of input channels must remain constant.
To display the spectra of signals in the Spectrum Analyzer:
Create the
dsp.SpectrumAnalyzerobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
scope = dsp.SpectrumAnalyzer creates a Spectrum Analyzer
System object. This object displays the frequency spectrum of real- and complex-valued
floating- and fixed-point signals.
scope = dsp.SpectrumAnalyzer(ports) creates a Spectrum Analyzer
object and sets the NumInputPorts property to the value of
ports.
scope = dsp.SpectrumAnalyzer(Name,Value) sets properties using
one or more name-value pairs. Enclose each property name in single quotes.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Frequently Used
Number of input ports, specified as a positive integer. Each signal coming through a separate input becomes a separate channel in the scope. You must invoke the scope with the same number of inputs as the value of this property.
The domain of the input signal you want to visualize, specified as
"Time" or "Frequency". If you visualize
time-domain signals, the Spectrum Analyzer transforms the signal to the frequency
spectrum based on the algorithm specified in the Method
property.
Scope Window Use
In the Estimation tab on the Spectrum Analyzer toolstrip, set
Input Domain to Time or
Frequency.
Data Types: char | string
Spectrum type, specified as one of these:
"Power" — Power spectrum
"Power density" — Power spectral density. The power spectral
density is the magnitude squared of the spectrum normalized to a bandwidth of 1
Hz.
"RMS" — Root mean square. The root mean square shows the square
root of the mean square. Use this option to view the frequency of voltage or current
signals.
Tunable: Yes
Dependency
To enable this property, set InputDomain to
"Time".
Scope Window Use
In the Scope tab on the Spectrum Analyzer toolstrip, select
Spectrum. Click Spectrum to select
Power, Power Density, or
RMS.
To enable these options, set the Input
Domain on the Estimation tab to
Time.
Data Types: char | string
Specify the spectrum type as one of "Spectrum",
"Spectrogram", or "Spectrum and spectrogram".
"Spectrum"— Shows the power spectrum."Spectrogram"— Shows frequency content over time. Each line of the spectrogram is one periodogram. Time scrolls from the bottom to the top of the display. The most recent spectrogram update is at the bottom of the display."Spectrum and Spectrogram"— Shows a dual view of a spectrum and spectrogram.
Tunable: Yes
Scope Window Use
In the Analyzer tab on the Spectrum Analyzer toolstrip, select Spectrum, Spectrogram, or both.
Data Types: char | string
Specify the sample rate, in hertz, of the input signals as a finite numeric scalar.
Scope Window Use
Open the Spectrum Settings. In the Main options section, set Sample rate (Hz).
Spectrum estimation method, specified as one of the following:
"Filter bank"–– Use an analysis filter bank to estimate the power spectrum. Compared to Welch's method, this method has a lower noise floor, better frequency resolution, and lower spectral leakage and requires fewer samples per update."Welch"–– Use Welch's method of averaged modified periodograms.
For more details on these methods, see Algorithms.
Tunable: Yes
Dependency
To enable this property, set InputDomain to
"Time".
Scope Window Use
In the Estimation tab of the Spectrum Analyzer toolstrip, set
Method to Filter bank or
Welch.
To enable this parameter, set Input Domain to
Time in the Estimation
tab.
Data Types: char | string
Option to plot a two-sided spectrum, specified as one of the following:
true— Compute and plot two-sided spectral estimates. When the input signal is complex valued, you must set this property totrue.false— Compute and plot one-sided spectral estimates. If you set this property tofalse, then the input signal must be real valued.When you set this property to
false, the Spectrum Analyzer uses power-folding. The y-axis values are twice the amplitude that they would be if you were to set this property totrue, except at0and the Nyquist frequency. A one-sided power spectral density (PSD) contains the total power of the signal in the frequency interval from DC to half the Nyquist rate. For more information, seepwelch.
Tunable: Yes
Scope Window Use
Click the Spectrum tab or the Spectrogram tab (if enabled) of the Spectrum Analyzer toolstrip. In the Trace Options section, select Two-Sided Spectrum to compute and plot two-sided spectral estimates.
Data Types: logical
Scale to display frequency, specified as one of the following:
"Linear"— Use a linear scale to display frequencies on the x-axis. To use the"Linear"setting, you must also set thePlotAsTwoSidedSpectrumproperty totrue."Log"— Use a logarithmic scale to display frequencies on the x-axis. To use the"Log"setting, you must also set thePlotAsTwoSidedSpectrumproperty tofalse.
Tunable: Yes
Scope Window Use
Click the Spectrum tab or the
Spectrogram tab (if enabled) of the Spectrum Analyzer
toolstrip. In the Scale section, set the Frequency
Scale to Linear or
Log.
To set the Frequency Scale to Log,
clear the Two-Sided Spectrum check box in the Trace
Options section in the Spectrum or the
Spectrogram tab (if enabled). If you select the
Two-Sided Spectrum check box, then you must set the
Frequency Scale to
Linear.
Data Types: char | string
Advanced
Frequency span mode, specified as one of the following:
"Full"–– The Spectrum Analyzer computes and plots the spectrum over the entire Nyquist Frequency Interval."Span and center frequency"–– The Spectrum Analyzer computes and plots the spectrum over the interval specified by theSpanandCenterFrequencyproperties."Start and stop frequencies"–– The Spectrum Analyzer computes and plots the spectrum over the interval specified by theStartFrequencyandStopFrequencyproperties.
Tunable: Yes
Dependency
To enable this property, set InputDomain to
"Time".
Scope Window Use
Click the Estimation tab on the Spectrum Analyzer toolstrip.
In the Frequency Options section, set Frequency
Span to Full, Span and Center
Frequency, or Start and Stop
Frequencies.
To enable the Frequency Span, set Input
Domain to Time.
Data Types: char | string
Specify the frequency span, in hertz, over which the Spectrum Analyzer computes
and plots the spectrum. The overall span, defined by this property and the
CenterFrequency property, must fall within the Nyquist Frequency Interval.
Tunable: Yes
Dependency
To enable this property, set FrequencySpan to
"Span and center frequency".
Scope Window Use
Open the Spectrum Settings. In the Main
options section, clear the Full frequency span
check box and set Span.
Start of the frequency interval over which spectrum is computed, specified in
hertz as a real scalar. The overall span, which is defined by this property and
StopFrequency, must fall within the Nyquist Frequency Interval.
Tunable: Yes
Dependency
To enable this property, set FrequencySpan to
"Start and stop frequencies".
Scope Window Use
Open the Spectrum Settings. In the Main
options section, clear the Full frequency span and
change Span to FStart. Set
FStart (Hz).
End of the frequency interval over which spectrum is computed, specified in hertz
as a real scalar. The overall span, which is defined by this property and the
StartFrequency property, must fall within the Nyquist Frequency Interval.
Tunable: Yes
Dependency
To enable this property, set FrequencySpan to
"Start and stop frequencies".
Scope Window Use
Open the Spectrum Settings. In the Main
options section, clear the Full frequency span and
change Span to FStart. Set
FStop (Hz).
Specify in hertz the center frequency of the span over which the Spectrum Analyzer
computes and plots the spectrum. The overall frequency span, defined by the
Span and this property, must fall within the Nyquist Frequency Interval.
Tunable: Yes
Dependency
To enable this property, set FrequencySpan to
"Span and center frequency".
Scope Window Use
Open the Spectrum Settings. In the Main, clear Full frequency span and set CF (Hz).
Frequency resolution method of the spectrum analyzer, specified as one of these options:
"rbw"–– TheRBWSourceandRBWproperties control the frequency resolution (in Hz) of the analyzer."num-frequency-bands"–– Applies only when you setMethodto"filter-bank". TheFFTLengthSourceandFFTLengthproperties control the frequency resolution."window-length"–– Applies only when you setMethodto"welch". TheWindowLengthproperty controls the frequency resolution.
Tunable: Yes
Dependency
To enable this property, set InputDomain to
"time".
Scope Window Use
Click the Estimation tab on the Spectrum Analyzer toolstrip. In the Frequency Resolution section, set Resolution Method to one of the available options.
Data Types: char | string
Specify the source of the resolution bandwidth (RBW) as either
"Auto" or "Property".
"Auto"— The Spectrum Analyzer adjusts the spectral estimation resolution to ensure that there are 1024 RBW intervals over the defined frequency span."Property"— Specify the resolution bandwidth directly using theRBWproperty.
Tunable: Yes
Dependency
To enable this property, set either:
InputDomainto"Time"andFrequencyResolutionMethodto"RBW".InputDomainto"Frequency".
Scope Window Use
Open the Spectrum Settings. In the Main options section, set RBW (Hz).
Data Types: char | string
RBW controls the spectral resolution of Spectrum Analyzer. Specify the resolution bandwidth in hertz as a real positive scalar. You must specify a value to ensure that there are at least two RBW intervals over the specified frequency span. Thus, the ratio of the overall span to RBW must be greater than two:
You can specify the overall span in different ways based on how you
set the FrequencySpan property.
Dependency
To enable, set:
RBWSourceto"Property"
Scope Window Use
Open the Spectrum Settings. In the Main options section, set RBW (Hz).
Control the frequency resolution by specifying the window length, in samples used to compute the spectral estimates. The window length must be an integer scalar greater than 2.
Tunable: Yes
Dependencies
To enable this property, set:
FrequencyResolutionMethodto"WindowLength", which controls the frequency resolution based on your window length settingMethodto"Welch"
Scope Window Use
Open the Spectrum Settings. Change the RBW
(Hz) dropdown to Window length.
Source of the FFT length, specified as one of these:
"auto"–– The value of FFT length depends on the setting of the frequency resolution method. When you set:FrequencyResolutionMethodto"rbw", the FFT length equals the number of samples per update, Nsamples. For more details on Nsamples, see the Algorithms section.FrequencyResolutionMethodto"window-length", the FFT length equals the value you specify in theWindowLengthproperty or 1024, whichever is larger.FrequencyResolutionMethodto"num-frequency-bands", the FFT length equals the input frame size (number of rows).
"property"–– The number of FFT points equals the value you specify in theFFTLengthproperty.
Tunable: Yes
Dependency
To enable this property, set:
Methodto"welch".Methodto"filter-bank"andFrequencyResolutionMethodto"num-frequency-bands".
Scope Window Use
Click the Estimation tab on the spectrum analyzer toolstrip.
In the Frequency Resolution section, set the FFT
Length to Auto or a positive
integer.
Data Types: char | string
Specify the length of the FFT that the Spectrum Analyzer uses to compute spectral estimates.
If FrequencyResolutionMethod is "RBW", the
FFT length is set as the window length required to achieve the specified resolution
bandwidth value or 1024, whichever is larger.
Tunable: Yes
Dependencies
To use this property, the following must be true:
FrequencyResolutionMethodis set to"WindowLength"or"NumFrequencyBands"FFTLengthis greater than or equal to theWindowLength.FFTLengthSourceis set to"Property".
Scope Window Use
Open the Spectrum Settings. In the Main
options section, next to the RBW (Hz) option,
enter a number or select Auto.
Specify the number of filter taps or coefficients for each frequency band. This
number must be a positive even integer. This value corresponds to the number of filter
coefficients per polyphase branch. The total number of filter coefficients is equal to
NumTapsPerBand + FFTLength.
Dependency
To enable this property, set Method to "Filter
Bank"
Scope Window Use
Open the Spectrum Settings. In the Main options section, set Taps per band.
"Auto"— The frequency vector is calculated from the length of the input. See Frequency Vector."Property"— Enter a custom vector as the frequency vector.
Dependency
To enable this property, set InputDomain to
"Frequency".
Scope Window Use
Open the Spectrum Settings. In the Frequency input options section, set Frequency (Hz).
Data Types: char | string
Custom frequency vector, specified as a monotonically increasing vector. This vector determines the x-axis of the display. The vector must be monotonically increasing and must have the same length as the input signal frame size.
Tunable: Yes
Dependency
To enable this property, set:
InputDomainto"Frequency".FrequencyVectorSourceto"Property".
Scope Window Use
Click the Estimation tab on the Spectrum Analyzer toolstrip. In the Domain section, set Frequency (Hz) to a monotonically increasing vector of length equal to the input signal frame size.
To enable the Frequency (Hz), set Input Domain
to Frequency.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
The percentage overlap between the previous and current buffered data segments, specified as a real, scalar value. The overlap creates a window segment that is used to compute a spectral estimate. The value must be greater than or equal to zero and less than 100.
Tunable: Yes
Scope Window Use
Open the Spectrum Settings. In the Window options section, set Overlap (%).
Specify a window function for the spectral estimator. The following table shows preset windows. For more information, follow the link to the corresponding function reference in the Signal Processing Toolbox™ documentation.
| Window Option | Corresponding Signal Processing Toolbox Function |
|---|---|
"Rectangular" | rectwin |
"Chebyshev" | chebwin |
"Flat Top" | flattopwin |
"Hamming" | hamming |
"Hann" | hann |
"Kaiser" | kaiser |
"Blackman-Harris" | blackmanharris |
To set your own spectral estimation window, set this property to
"Custom" and specify a custom window function in the CustomWindow property.
Tunable: Yes
Dependency
To enable this property, set:
InputDomainto"Time".Methodto"Welch"
Scope Window Use
Click the Estimation tab on the Spectrum Analyzer toolstrip. In the Window Options section, set the Window.
To enable the Window, set Input Domain
to Time and Method to
Welch in the Estimation tab on
the Spectrum Analyzer toolstrip.
Data Types: char | string
Name of the custom window function, specified as a character vector or string scalar. The name of the custom window function must be on the MATLAB path. Use this property if you want to customize the window using additional properties available with the Signal Processing Toolbox version of the window function.
Tunable: Yes
Example
Define and use a custom window function.
function w = my_hann(L) w = hann(L, 'periodic') end scope.Window = 'Custom'; scope.CustomWindow = 'my_hann'
Dependency
To use this property, set Window to
"Custom".
Scope Window Use
Click the Estimation tab on the Spectrum Analyzer toolstrip. In the Window Options section, for the Window, enter the name of the custom window function.
Data Types: char | string
The window sidelobe attenuation, in decibels (dB). The value must be greater than
or equal to 45.
Tunable: Yes
Dependency
To enable this property, set Window to
"Chebyshev" or "Kaiser".
Scope Window Use
Open the Spectrum Settings. In the Window options section, set Attenuation (dB).
Select the units of the frequency-domain input. This property allows the Spectrum
Analyzer to scale frequency data if you choose a different display unit with the
SpectrumUnits property.
Dependency
This option is only available when InputDomain is set to
Frequency.
Scope Window Use
Open the Spectrum Settings. In the Frequency input options section, set Input units.
Data Types: char | string
Specify the units in which the Spectrum Analyzer displays power values.
Tunable: Yes
Dependency
The spectrum units available depend on the value you specify in the
SpectrumType property.
InputDomain | SpectrumType | Allowed
SpectrumUnits |
|---|---|---|
"Time" | "Power" | "dBm", "dBW",
"dBFS",
"Watts" |
"Power density" | "dBm/Hz",
"dBW/Hz","dBFS/Hz",
"Watts/Hz" | |
"RMS" | "dBV", "Vrms" | |
"Frequency" | ― | "Auto",
"dBm", "dBV",
"dBW", "Vrms",
"Watts" |
If you set the InputDomain property to
"Frequency" and the SpectrumUnits
property to "Auto", the Spectrum Analyzer assumes the spectrum
units to be equal to input units specified in the InputUnits
property. If you set InputDomain to "Time"
and SpectrumUnits to any option other than
"Auto", then the Spectrum Analyzer converts the units
specified in InputUnits to the units specified in
SpectrumUnits.
Scope Window Use
Click the Spectrum tab on the Spectrum Analyzer toolstrip. In the Scale section, set Spectrum Unit.
Data Types: char | string
Specify the source of the dBFS scaling factor as either "Auto" or
"Property".
"Auto"–– The Spectrum Analyzer adjusts the scaling factor based on the input data."Property"–– Specify the full-scale scaling factor using theFullScaleproperty.
Tunable: Yes
Dependency
To enable this property, set:
InputDomainto"Time"SpectrumTypeto"Power"or"Power density"SpectrumUnitsto"dBFS"or"dBFS/Hz"(when spectrum type is set to"Power density")
Scope Window Use
Click the Spectrum tab on the Spectrum Analyzer toolstrip. In
the Scale section, set the Full Scale to
either Auto or a positive scalar.
To enable the Full Scale:
In the Analyzer tab, set the spectrum type to
PowerorPower Density.In the Estimation tab, set Input Domain to
Time.In the Spectrum tab, set Spectrum Unit to
dBFSordBFS/Hz(when spectrum type is set toPower Density).
Data Types: char | string
Specify a real positive scalar for the dBFS full scale.
Tunable: Yes
Dependency
To enable this option set:
SpectrumUnitsto"dBFS"FullScaleSourceto"Property"
Scope Window Use
Open the Spectrum Settings. In the Trace
options section, set Full scale to
Auto or enter a number.
Averaging method, specified as one of the following:
"VBW"— Video bandwidth method. The object uses a lowpass filter to smooth the trace and decrease noise. Use theVBWSourceandVBWproperties to specify the VBW value."Exponential"— Weighted average of samples. The object computes the average over samples weighted by an exponentially decaying forgetting factor. Use theForgettingFactorproperty to specify the weighted forgetting factor.
For more information, see Averaging Method.
Tunable: Yes
Dependency
To enable this property, set InputDomain to
"Time".
Scope Window Use
Click the Estimation tab on the Spectrum Analyzer
toolstrip. In the Averaging section, set
Averaging Method to
VBW or
Exponential.
To enable the Averaging Method, set
Input Domain to
Time.
Data Types: char | string
The Spectrum Analyzer computes the current power spectrum estimate by computing a running average of the last N power spectrum estimates. This property defines N.
Tunable: Yes
Dependency
To enable this property, set ViewType to
"Spectrum".
Dependency
This property applies only when the AveragingMethod is
"Running".
Scope Window Use
Open the Spectrum Settings. In the Trace options section, set Averages.
Specify the exponential weighting as a scalar value greater than 0 and less than or equal to 1.
Dependency
This property applies only when the AveragingMethod is
"Exponential".
Scope Window Use
Open the Spectrum Settings. In the Trace options section, set Forgetting factor.
The load the scope uses as a reference to compute power levels.
Tunable: Yes
Scope Window Use
Open the Spectrum Settings. In the Trace options section, set Ref. load (Ohms).
Scalar — Apply the same frequency offset to all channels, specified in hertz as a character vector.
Vector — apply a specific frequency offset for each channel, specify a vector of frequencies. The vector length must be equal to number of input channels.
The frequency-axis values are offset by the values specified in this property. The overall span must fall within the Nyquist Frequency Interval. You can control the overall span in different ways based on how you set the
FrequencySpanproperty.
Tunable: Yes
Scope Window Use
Open the Spectrum Settings. In the Trace options section, set Offset (Hz).
Spectrogram
Specify the channel for which the spectrogram is plotted, as a real, positive scalar integer in the range [1 N], where N is the number of input channels.
Tunable: Yes
Dependency
To enable this property, set ViewType to
"Spectrogram" or "Spectrum and
spectrogram".
Scope Window Use
Open the Spectrum Settings. In the Spectrogram options section, select a Channel.
Specify the source for the time resolution of each spectrogram line as either
"Auto" or "Property". The TimeResolution property shows the time resolution for the different
frequency resolution methods and time resolution properties.
Tunable: Yes
Dependency
To enable this property, set ViewType to
"Spectrogram" or "Spectrum and
spectrogram".
Scope Window Use
Click the Spectrogram tab on the Spectrum Analyzer toolstrip.
In the Time Options section, set the Time Resolution
(s) to Auto or enter a positive scalar.
To enable the Time Resolution (s), select Spectrogram in the Analyzer tab.
Data Types: char | string
Specify the time resolution of each spectrogram line as a positive scalar, expressed in seconds.
The Spectrum Analyzer determines the time resolution value based on the frequency resolution method, RBW, and time resolution properties.
| Method | RBW | Time Resolution | Resulting Time Resolution in Seconds |
|---|---|---|---|
Welch or Filter
Bank | Auto | Auto | 1/RBW |
Welch or Filter
Bank | Auto | Manually entered | 1/Time Resolution Hz |
Welch or Filter
Bank | Manually entered | Auto | 1/RBW seconds |
Welch or Filter
Bank | Manually entered | Manually entered | Equal to or greater than the minimum attainable time resolution 1/RBW. The Spectrum Analyzer combines several spectral estimates into one spectrogram line to obtain the desired time resolution. It uses interpolation to obtain time resolution values that are not integer multiples of 1/RBW. |
Tunable: Yes
Dependency
To enable this property, set:
ViewTypeto"Spectrogram"or"Spectrum and spectrogram"TimeResolutionSourceto"Property.
Scope Window Use
Open the Spectrum Settings. In the Spectrogram options section, in the Time res (s) box, enter a number.
Source for the time span of the spectrogram, specified as either
"Auto" or "Property". If you set this property
to "Auto", the spectrogram displays 100 spectrogram lines at any
given time. If you set this property to "Property", the spectrogram
uses the time duration you specify in seconds in the TimeSpan property.
Tunable: Yes
Dependency
To enable this property, set ViewType to
"Spectrogram" or "Spectrum and
spectrogram".
Scope Window Use
Click the Spectrogram tab on the Spectrum Analyzer toolstrip.
In the Time Options section, set the Time Span
(s) to Auto or enter a positive scalar.
Data Types: char | string
Specify the time span of the spectrogram display in seconds. You must set the time span to be at least twice as large as the duration of the number of samples required for a spectral update.
Tunable: Yes
Dependency
To enable this property, set:
ViewTypeto"Spectrogram"or"Spectrum and spectrogram".TimeSpanSourceto"Property".
Scope Window Use
Open the Spectrum Settings. In the Spectrogram options section, in the Time span (s) box, enter a number.
Measurements
Channel for which the measurements are obtained, specified as a real, positive integer greater than 0 and less than or equal to 100. The maximum number you can specify is the number of channels (columns) in the input signal.
Tunable: Yes
Scope Window Use
Click on Tools > Measurements and open the Trace Selection settings.
Data Types: double
Specify whether to display upper and lower spectral mask lines on a spectrum plot.
This property uses properties from a SpectralMaskSpecification object to enable and configure the spectral
masks.
Tunable: Yes
Scope Window Use
Open the Spectral Mask pane and modify the Settings options.
Peak finder measurement, specified as a PeakFinderConfiguration object. Enable peak finder to compute and display
the largest calculated peak values. All PeakFinderConfiguration
properties are tunable.
Tunable: Yes
Dependency
To enable this property, set ViewType to
"Spectrum" or "Spectrum and
spectrogram".
Scope Window Use
Click the Measurements tab on the Spectrum Analyzer toolstrip and modify the peak finder measurements in the Peaks section.
The Measurements tab appears when you select Spectrum in the Scope tab.
Cursor measurements, specified as a CursorMeasurementsConfiguration
object. Enable cursor measurements to display waveform cursors. All
CursorMeasurementsConfiguration properties are
tunable.
Tunable: Yes
Dependency
To enable this property, set ViewType to "Spectrum" or
"Spectrum and spectrogram".
Scope Window Use
Click the Measurements tab on the Spectrum Analyzer toolstrip and modify the cursor measurements in the Cursors section.
The Measurements tab appears when you select Spectrum in the Scope tab.
Enable channel measurements to compute and display the occupied bandwidth or adjacent channel power ratio. The ChannelMeasurements property uses the ChannelMeasurementsSpecification properties.
The ChannelMeasurementsSpecification properties are:
Algorithm–– Type of measurement data to display, specified as either"Occupied BW"or"ACPR".Default:
"Occupied BW"FrequencySpan–– Frequency span mode, specified as either"Span and center frequency"or"Start and stop frequencies"Default:
"Span and center frequency"Span–– Frequency span over which the channel measurements are computed, specified as a real, positive scalar in Hz. This property applies when you set theFrequencySpanproperty to"Span and center frequency".Default:
2000HzCenterFrequency–– Center frequency of the span over which the channel measurements are computed, specified as a real scalar in Hz. This property applies when you set theFrequencySpanproperty to"Span and center frequency".Default:
0HzStartFrequency–– Start frequency over which the channel measurements are computed, specified as a real scalar in Hz. This property applies when you set theFrequencySpanproperty to"Start and stop frequencies".Default:
-1000HzStopFrequency–– Stop frequency over which the channel measurements are computed, specified as a real scalar in Hz. This property applies when you set theFrequencySpanproperty to"Start and stop frequencies".Default:
1000HzPercentOccupiedBW–– Percent of power over which to compute the occupied bandwidth, specified as a positive real scalar. This property applies when you set theAlgorithmproperty to"Occupied BW".Default:
99NumOffsets–– Number of adjacent channel pairs, specified as a real, positive integer. This property applies when you set theAlgorithmproperty to"ACPR".Default:
2AdjacentBW–– Adjacent channel bandwidth, specified as a real, positive scalar. This property applies when you set theAlgorithmproperty to"ACPR".Default:
1000FilterShape–– Filter shape for both main and adjacent channels, specified as"None","Gaussian", or"RRC". This property applies when you set theAlgorithmproperty to"ACPR".Default:
"None"FilterCoeff–– Channel filter coefficient, specified as a real scalar between0and1. This property applies when you set theAlgorithmproperty to"ACPR"and theFilterShapeproperty to either"Gaussian"or"RRC".Default:
0.5ACPROffsets–– Frequency of the adjacent channel relative to the center frequency of the main channel, specified as a real vector of length equal to the number of offset pairs specified inNumOffsets. This property applies when you set theAlgorithmproperty to"ACPR".Default:
[2000 3500]Enable–– Set this property totrueto enable channel measurements. Valid values aretrueorfalse.Default:
false
All ChannelMeasurementsSpecification properties are tunable.
Scope Window Use
Open the Channel Measurements pane (![]() ) and modify the Measurement
and Channel Settings options.
) and modify the Measurement
and Channel Settings options.
Distortion measurements, specified as a DistortionMeasurementsConfiguration object. Enable distortion measurements
to compute and display the harmonic distortion and intermodulation distortion. All
DistortionMeasurementsConfiguration properties are tunable.
Tunable: Yes
Dependency
To enable this property, set ViewType to "Spectrum" or
"Spectrum and spectrogram".
Scope Window Use
Click the Measurements tab on the Spectrum Analyzer toolstrip and modify the distortion measurements in the Distortion section.
The Measurements tab appears when you select Spectrum in the Scope tab.
Visualization
Caption to display in the scope window, specified as a character vector or string scalar.
Tunable: Yes
Data Types: char | string
Spectrum Analyzer window position in pixels, specified by the size and location of the scope window as a four-element double vector of the form [left bottom width height]. You can place the scope window in a specific position on your screen by modifying the values to this property.
By default, the window appears in the center of your screen with a width of 800 pixels and height
of 450 pixels. The exact center coordinates depend on your screen resolution.
Tunable: Yes
Plot type to display normal traces, specified as "Line",
"Stem", a cell array of these character vectors, or an array of
these strings. Normal traces are traces that display free-running spectral
estimates.
You can individually control the type of plot
for each line by specifying the PlotType property as a cell array
of character vectors or an array of strings. (since R2025a)
Tunable: Yes
Dependencies
To enable this property, set:
ViewTypeto"Spectrum"or"Spectrum and spectrogram".PlotNormalTracetotrue.
Scope Window Use
Click the Scope tab on the Spectrum Analyzer toolstrip,
navigate to the Configuration section and click
Settings. In the Spectrum Analyzer Settings window, under
Display and Labels, set Plot Type to
Line or Stem.
To enable the Plot Type, you must:
Select Spectrum in the Views section of the Scope tab.
Enable the Normal Trace check box in the Trace Options section of the Spectrum tab.
Data Types: char | string
To remove normal traces from the display, set this property to
false. These traces display the free-running spectral estimates.
The Spectrum Analyzer continues its spectral computations even when you set this
property to false.
Tunable: Yes
Dependency
To enable this property, set ViewType to
"Spectrum" or "Spectrum and
spectrogram".
Scope Window Use
Click the Spectrum tab on the Spectrum Analyzer toolstrip and select the Normal Trace check box in the Trace Options section.
To enable the Normal Trace check box, select Spectrum in the Analyzer tab.
Data Types: logical
To compute and plot the maximum-hold spectrum of each input channel, set this property to true.
The maximum-hold spectrum at each frequency bin is computed by keeping the maximum value of all the power spectrum
estimates. When you toggle this property, the Spectrum Analyzer resets its maximum-hold computations.
Tunable: Yes
Dependency
To enable this property, set ViewType to
"Spectrum" or "Spectrum and
spectrogram".
Scope Window Use
Click the Spectrum tab on the Spectrum Analyzer toolstrip and select the Max-Hold Trace check box in the Trace Options section.
To enable the Max-Hold Trace check box, select Spectrum in the Analyzer tab.
Data Types: logical
To compute and plot the minimum-hold spectrum of each input channel, set this property to true.
The minimum-hold spectrum at each frequency bin is computed by keeping the minimum value of all the power spectrum
estimates. When you toggle this property, the Spectrum Analyzer resets its minimum-hold computations.
Tunable: Yes
Dependency
To enable this property, set ViewType to
"Spectrum" or "Spectrum and
spectrogram".
Scope Window Use
Click the Spectrum tab on the Spectrum Analyzer toolstrip and select the Min-Hold Trace check box in the Trace Options section.
To enable the Min-Hold Trace check box, select Spectrum in the Analyzer tab.
Data Types: logical
Display title, specified as a character vector or a string scalar.
Tunable: Yes
Scope Window Use
Click the Scope tab on the spectrum analyzer toolstrip. In the Configuration section, click Settings, and enter Title.
Data Types: char | string
y-axis label, specified as a character vector or a string scalar. The Spectrum Analyzer displays the label to the left of the y-axis.
Regardless of the value of this property, Spectrum Analyzer always displays power
units as one of the SpectrumUnits values.
Tunable: Yes
Dependency
To enable this property, set ViewType to
"Spectrum" or "Spectrum and
spectrogram".
Scope Window Use
Click the Scope tab on the Spectrum Analyzer toolstrip. In the Configuration section, click Settings. In the Spectrum Analyzer Settings window that opens up, under Display and labels, enter Y-Label.
To enable the Y-Label, select Spectrum in the Scope tab.
Data Types: char | string
Flag to show the legend, specified as true or
false. To show a legend with the input names, set this property
to true.
Use the legend to control which signals are visible. In the scope legend, click a signal name to hide the signal in the scope. To show the signal, click the signal name again. To show only one signal, right-click the signal name. To show all signals, press Esc.
Tunable: Yes
Dependencies
To enable this property, set the ViewType property to
"Spectrum" or "Spectrum and spectrogram".
Scope Window Use
Click the Scope tab on the Spectrum Analyzer toolstrip. To see the legend, click Legend in the Configuration section.
To enable the Legend, select Spectrum in the Scope tab.
Data Types: logical
Channel names in the input data, specified as a cell array of character vectors or an array of strings. The names you specify in this property appear in the following locations:
Legend
Spectrum Analyzer Settings > Color and styling section
Measurements and Channel Measurements tabs
If you do not specify channel names, the
spectrum analyzer names the channels as Channel 1, Channel
2, and so on.
Tunable: Yes
Dependency
To see the channel names, set ShowLegend to
true.
Scope Window Use
Click the Scope tab on the spectrum analyzer toolstrip. To see the legend, click Legend in the Configuration section.
Data Types: char
Flag to show the grid, specified as true or
false. Set this property to true to show grid
lines in the plot.
Tunable: Yes
Scope Window Use
Click the Scope tab on the Spectrum Analyzer toolstrip. In the Configuration section, click Settings, and select Show Grid.
Data Types: logical
y-axis limits, specified as a two-element numeric vector of the
form [ymin ymax]. The units of the y-axis limits
depend on the SpectrumUnits property.
Example: scope.YLimits = [-10,20]
Tunable: Yes
Dependencies
To enable this property, set the
ViewTypeproperty to"Spectrum"or"Spectrum and spectrogram".The units directly depend upon the
SpectrumUnitsproperty.
Scope Window Use
Click the Scope tab on the Spectrum Analyzer toolstrip. In the Configuration section, click Settings. In the Spectrum Analyzer Settings window that opens up, under Display and Labels, enter Y-Limits.
To enable the Y-Limits, select Spectrum in the Scope tab.
Color limits of the spectrogram, specified as a two-element numeric vector of the form
[colorMin colorMax]. The units of the color limits directly
depend upon the SpectrumUnits property.
Example: scope.ColorLimits = [-10,20]
Tunable: Yes
Dependencies
To enable this property, set the
ViewTypeproperty to"Spectrogram"or"Spectrum and spectrogram".The units directly depend upon the
SpectrumUnitsproperty.
Scope Window Use
Click the Analyzer tab on the Spectrum Analyzer toolstrip. In the Configuration section, click Settings. In the Spectrum Analyzer Settings window that opens up, under Display and Labels, enter Color Limits.
To enable the Color Limits, select Spectrogram in the Analyzer tab.
Axes scaling mode, specified as one of these:
"Auto"— The scope scales the axes to fit the data, both during and after simulation."Manual"— The scope does not scale the axes automatically."OnceAtStop"— The scope scales the axes when the simulation stops."Updates"— The scope scales the axes after a specific number of visual updates. It determines the number of updates using theAxesScalingNumUpdatesproperty.
Tunable: Yes
Data Types: char | string
Layout of the axes, specified as one of "Vertical" or
"Horizontal". A vertical layout stacks the spectrum above the
spectrogram. A horizontal layout puts the two views side-by-side.
Tunable: Yes
Dependency
To enable this property, set ViewType to "Spectrum
and spectrogram".
Scope Window Use
Click the Analyzer tab on the Spectrum Analyzer toolstrip. Select Spectrum and Spectrogram. In the Configuration section, select and update Layout.
Data Types: char | string
Usage
Description
scope( updates the spectrum of the
signal in the spectrum analyzer.signal)
scope(signal1,signal2,...,signalN) displays multiple signals in
the spectrum analyzer. The signals must have the same frame length, but can vary in number
of channels. You must set the NumInputPorts property to enable
multiple input signals.
Input Arguments
Specify one or more input signals to visualize in the
dsp.SpectrumAnalyzer. Signals can have a different number of channels, but
must have the same frame length.
Example: scope(signal1, signal2)
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fi
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
generateScript | Generate MATLAB script to create scope with current settings |
getMeasurementsData | Get the current measurement data displayed on the spectrum analyzer |
getSpectralMaskStatus | Get test results of current spectral mask |
getSpectrumData | Save spectrum data shown in spectrum analyzer |
isNewDataReady | Check spectrum analyzer for new data |
If you want to restart the simulation from the beginning, call reset to
clear the scope window displays. Do not call reset after calling
release.
Examples
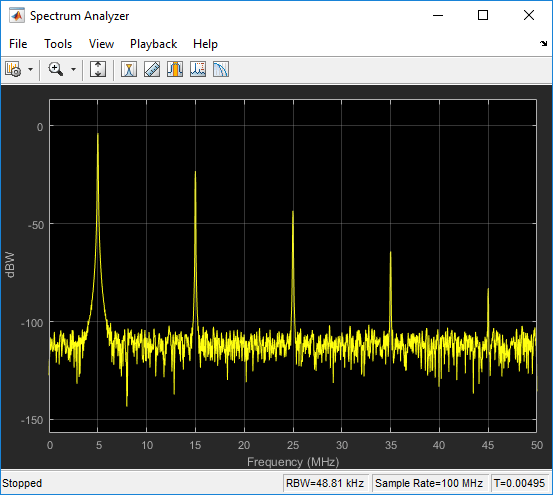
View a one-sided power spectrum made from the sum of fixed real sine waves with different amplitudes and frequencies.
Fs = 100e6; % Sampling frequency fSz = 5000; % Frame size sin1 = dsp.SineWave(1e0, 5e6,0,'SamplesPerFrame',fSz,'SampleRate',Fs); sin2 = dsp.SineWave(1e-1,15e6,0,'SamplesPerFrame',fSz,'SampleRate',Fs); sin3 = dsp.SineWave(1e-2,25e6,0,'SamplesPerFrame',fSz,'SampleRate',Fs); sin4 = dsp.SineWave(1e-3,35e6,0,'SamplesPerFrame',fSz,'SampleRate',Fs); sin5 = dsp.SineWave(1e-4,45e6,0,'SamplesPerFrame',fSz,'SampleRate',Fs); scope = dsp.SpectrumAnalyzer; scope.SampleRate = Fs; scope.SpectralAverages = 1; scope.PlotAsTwoSidedSpectrum = false; scope.RBWSource = 'Auto'; scope.PowerUnits = 'dBW'; for idx = 1:1e2 y1 = sin1(); y2 = sin2(); y3 = sin3(); y4 = sin4(); y5 = sin5(); scope(y1+y2+y3+y4+y5+0.0001*randn(fSz,1)); end
Run the release method to let property values and input
characteristics change. The scope automatically scales the axes.
release(scope)
Run the clear function to close the Spectrum Analyzer
window.
clear('scope');View a two-sided power spectrum of a sine wave with noise on the Spectrum Analyzer.
sin = dsp.SineWave('Frequency',100,'SampleRate',1000); sin.SamplesPerFrame = 1000; scope = dsp.SpectrumAnalyzer('SampleRate',sin.SampleRate); for ii = 1:250 x = sin() + 0.05*randn(1000,1); scope(x); end
Run the release method to change property values and input
characteristics. The scope automatically scales the axes. It updates the display one
more time if any data is in the internal buffer.
release(scope);
Run the MATLAB clear function to close the Spectrum Analyzer
window.
clear('scope');This example shows the spectrogram for a chirp signal with added random noise.
Fs = 233e3; frameSize = 20e3; chirp = dsp.Chirp('SampleRate',Fs,... 'SamplesPerFrame',frameSize,... 'InitialFrequency',11e3,... 'TargetFrequency',11e3+55e3); scope = dsp.SpectrumAnalyzer('SampleRate',Fs); scope.ViewType = 'Spectrogram'; scope.RBWSource = 'Property'; scope.RBW = 500; scope.TimeSpanSource = 'Property'; scope.TimeSpan = 2; scope.PlotAsTwoSidedSpectrum = false; for idx = 1:50 y = chirp()+ 0.05*randn(frameSize,1); scope(y); end release(scope)
Use the Spectrum Analyzer to display frequency input from spectral estimates of sinusoids embedded in white Gaussian noise.
Initialization
Initialize two dsp.SpectrumEstimator objects to display. Set one
object to use the Welch-based spectral estimation technique with a Hann window, set the
other object use a filter bank estimation. Specify a noisy sine wave input signal with
four sinusoids at 0.16, 0.2, 0.205, and 0.25 cycles/sample. View the spectral estimate
using a third object, a spectrum analyzer, set to process frequency input.
FrameSize = 420; Fs = 1; Frequency = [0.16 0.2 0.205 0.25]; sinegen = dsp.SineWave('SampleRate',Fs,'SamplesPerFrame',FrameSize,... 'Frequency',Frequency,'Amplitude',[2e-5 1 0.05 0.5]); NoiseVar = 1e-10; numAvgs = 8; hannEstimator = dsp.SpectrumEstimator('PowerUnits','dBm',... 'Window','Hann','FrequencyRange','onesided',... 'SpectralAverages',numAvgs,'SampleRate',Fs); filterBankEstimator = dsp.SpectrumEstimator('PowerUnits','dBm',... 'Method','Filter bank','FrequencyRange','onesided',... 'SpectralAverages',numAvgs,'SampleRate',Fs); spectrumPlotter = dsp.SpectrumAnalyzer('InputDomain','Frequency',... 'SampleRate',Fs,... 'SpectrumUnits','dBm','YLimits',[-120,40],... 'PlotAsTwoSidedSpectrum',false,... 'ChannelNames',{'Hann window','Filter bank'},'ShowLegend',true);
Streaming
Stream the input. Compare the spectral estimates in the spectrum analyzer.
for i = 1:1000 x = sum(sinegen(),2) + sqrt(NoiseVar)*randn(FrameSize,1); Pse_hann = hannEstimator(x); Pfb = filterBankEstimator(x); spectrumPlotter([Pse_hann,Pfb]) end
Compute and display the power spectrum of a noisy sinusoidal input
signal using the dsp.SpectrumAnalyzer
System object. Measure the peaks, cursor placements, adjacent channel power ratio, and
distortion in the spectrum by enabling the following properties:
PeakFinderCursorMeasurementsChannelMeasurementsDistortionMeasurements
Initialization
The input sine wave has two frequencies: 1000 Hz and 5000 Hz. Create two
dsp.SineWave System objects to generate these two frequencies.
Create a dsp.SpectrumAnalyzer System object to compute and display
the power spectrum.
Fs = 44100; Sineobject1 = dsp.SineWave('SamplesPerFrame',1024,... 'PhaseOffset',10,... 'SampleRate',Fs,'Frequency',1000); Sineobject2 = dsp.SineWave('SamplesPerFrame',1024,... 'SampleRate',Fs,'Frequency',5000); SA = dsp.SpectrumAnalyzer('SampleRate',Fs,'Method','Filter bank',... 'SpectrumType','Power','PlotAsTwoSidedSpectrum',false,... 'ChannelNames',{'Power spectrum of the input'},... 'YLimits',[-120 40],'ShowLegend',true);
Enable Measurements Data
To obtain the measurements, set the Enable property of the
measurements to true.
SA.CursorMeasurements.Enable = true; SA.ChannelMeasurements.Enable = true; SA.PeakFinder.Enable = true; SA.DistortionMeasurements.Enable = true;
Use getMeasurementsData
Stream in the noisy sine wave input signal and estimate the power spectrum of the
signal using the spectrum analyzer. Measure the characteristics of the spectrum. Use the
getMeasurementsData function to obtain these measurements
programmatically. The isNewDataReady function indicates when there is
new spectrum data. The measured data is stored in the variable
data.
data = []; for Iter = 1:1000 Sinewave1 = Sineobject1(); Sinewave2 = Sineobject2(); Input = Sinewave1 + Sinewave2; NoisyInput = Input + 0.001*randn(1024,1); SA(NoisyInput); if SA.isNewDataReady data = [data;getMeasurementsData(SA)]; end end
The right side of the spectrum analyzer shows the enabled measurement panes. The
values shown in these panes match with the values shown in the last time step of the
data variable. You can access the individual fields of
data to obtain the various measurements programmatically.
Compare Peak Values
Peak values are obtained by the PeakFinder property. Verify that
the peak values obtained in the last time step of data match the
values shown on the spectrum analyzer plot.
peakvalues = data.PeakFinder(end).Value
peakvalues = 3×1
26.9851
24.1735
-51.1973
frequencieskHz = data.PeakFinder(end).Frequency/1000
frequencieskHz = 3×1
4.9957
0.9905
0.2369
Tips
To close the scope window and clear its associated data, use the MATLAB
clearfunction.To hide or show the scope window, use the
hideandshowfunctions.Use the MATLAB
mccfunction to compile code containing a Spectrum Analyzer.You cannot open Spectrum Analyzer configuration dialog boxes if you have more than one compiled component in your application.
Algorithms
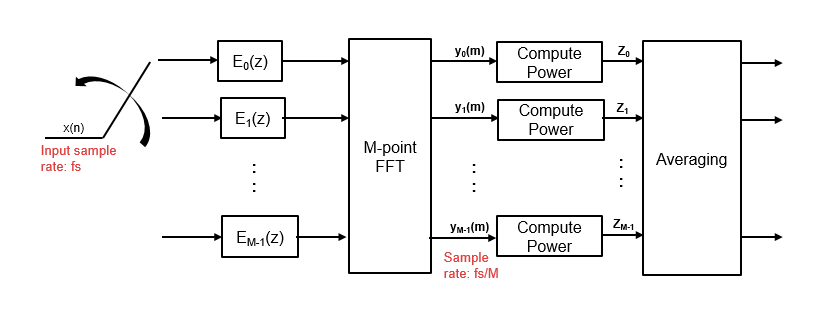
When you choose the Filter Bank method, the spectrum
analyzer uses an analysis filter bank to estimate the power spectrum.
The filter bank splits the broadband input signal x(n), of sample rate fs, into multiple narrow band signals y0(m), y1(m), … , yM-1(m), of sample rate fs/M.
The variable M represents the number of frequency bands in the
filter bank. In the spectrum analyzer, M is equal to the number of
data points needed to achieve the specified RBW value or 1024, whichever is larger. For
more information on the analysis filter bank and its implementation, see the More About and the Algorithm sections in the
dsp.Channelizer object.
After the spectrum analyzer splits the broadband input signal into multiple narrow bands, it computes the power in each narrow frequency band using the following equation. Each Zi value is the power estimate over that narrow frequency band.
L is length of the narrowband signal yi(m) and i = 1, 2, …, M−1.
The power values in all the narrow frequency bands (denoted by Zi) form the Z vector.
The spectrum analyzer averages the current Z vector with the previous Z vectors using one of the moving average methods: video bandwidth, exponential weighting, or running. The output of the averaging operation forms the spectral estimate vector. For details on the two averaging methods, see Averaging Method.
The spectrum analyzer uses the value you specify in the RBW (Hz) parameter or the Number of frequency bands parameter to determine the input frame length.
When you specify the Resolution Method to
RBW, and you set RBW (Hz) to:
Auto–– The spectrum analyzer determines the appropriate resolution bandwidth to ensure that there are 1024 RBW intervals over the specified frequency span. When you set RBW (Hz) toAuto, the spectrum analyzer calculates RBW using this equation.scalar value –– The spectrum analyzer calculates the number of samples Nsamples using this equation.
Fs is the sample rate of the input signal as specified in the Sample Rate (Hz) property.
The RBW value you specify must be such that there are at least two RBW intervals over the specified frequency span. The ratio of the overall span to RBW must be greater than two.
span is the frequency span over which the spectrum analyzer computes and plots the spectrum. To view the Span (Hz) in the scope, click the Estimation tab on the spectrum analyzer toolstrip and navigate to the Frequency Options section. To enable this property, set Frequency Span to
Span and Center Frequency.
When you specify the Resolution Method to Number of
frequency bands, the resulting RBW is given by:
When the number of input samples is not sufficient to achieve the specified resolution bandwidth, the spectrum analyzer adjusts its RBW value according to the number of input samples provided and displays a message similar to this one. The spectrum analyzer removes this message once you provide enough input samples.

When you select the Welch method, the power spectrum estimate is
the averaged modified periodograms.
The algorithm in the spectrum analyzer consists of these steps:
The block buffers the input into N-point data segments. Each data segment is split into P overlapping data segments, each of length M, overlapping by D points. The data segments can be represented as:
If D = M/2, the overlap is 50%.
If D = 0, the overlap is 0%.
Apply a window to each of the P overlapping data segments in the time domain.
If you set the Resolution Method to
Window length, you can specify the data window length Nwindow using the Window Length parameter in the Estimation tab.If you set the Resolution Method to
RBW, the algorithm determines the data window length using this equation, .Then, it partitions the input signal into a number of windowed data segments.
Most window functions afford more influence to the data at the center of the set than to the data at the edges, which represents a loss of information. To mitigate that loss, the individual data sets are commonly overlapped in time. For each windowed segment, compute the periodogram by computing the discrete Fourier transform. Then compute the squared magnitude of the result and divide the result by M.
where U is the normalization factor for the power in the window function and is given by
You can specify the window using the Window parameter in the Estimation tab of the spectrum analyzer toolstrip.
The spectrum analyzer calculates and plots the power spectrum, power spectrum density, and RMS using the modified Periodogram estimator. For more information about the Periodogram method, see
periodogram.To determine the power spectrum estimate for Welch's method, the spectrum analyzer averages the result of the periodograms for the last P data segments. The averaging reduces the variance, compared to the original N-point data segment. For more details on the averaging, see Averaging Method.
The spectrum analyzer computes the power spectral density using:
The power spectrum is the product of the power spectral density and the resolution bandwidth, as given by this equation.
The spectrum analyzer plots the power as a spectrogram in the Spectrogram mode. Each line of the spectrogram is one periodogram. The time resolution of each line is 1/RBW, which is the minimum attainable resolution. Achieving the resolution you want might require combining several periodograms. You then use interpolation to calculate noninteger values of 1/RBW. In the spectrogram display, time scrolls from top to bottom, so the most recent data appears at the top of the display. The offset shows the time value at which the center of the most current spectrogram line occurred.
The spectrum analyzer uses a certain number of samples to compute a spectral estimate. This value is directly related to the resolution bandwidth (RBW) using this equation,
or to the window length (Nwindow) using this equation,
where Op is the overlap percentage, NENBW is the normalized effective noise bandwidth, Fs is the input sample rate, and RBW is the resolution bandwidth.
The spectrum analyzer shows the number of samples per update in the spectrum analyzer status bar.
When you specify the Resolution
Method to RBW, the window length is given
by,
When you specify the Resolution
Method to Window length, the algorithm uses
the window length value you specify in the Window Length parameter
in the Estimation tab on the spectrum analyzer toolstrip.
The overlap percentage Op is the value you specify in the Overlap % property. To view the Overlap % in the scope, click the Estimation tab on the spectrum analyzer toolstrip and navigate to the Window Options section.
When you increase the overlap percentage, the spectrum analyzer needs fewer new input samples to compute a new spectral update.
| Op | Nsamples |
|---|---|
| 0% | 100 |
| 50% | 50 |
| 80% | 20 |
The normalized effective noise bandwidth NENBW is a window parameter that measures the noise performance of the window. NENBW is determined using the window length and the window coefficients, and is given by the following equation:
w(n) denotes the vector of window coefficients. Nwindow is the window length. For more information on how the algorithm determines the window length, see the Spectrum Estimation –– Welch's Method section in Algorithms.
The rectangular window has the smallest NENBW, with a value of 1. All other windows have a larger NENBW value. For example, the Hann window has an NENBW value of approximately 1.5.
The spectrum analyzer shows the value of NENBW in the spectrum analyzer status bar.
You can enable NENBW only when you set
Input Domain to Time and
Estimation Method to Welch in the
Estimation tab on the spectrum analyzer toolstrip.
Fs is the sample rate of the input signal.
To view the Sample Rate (Hz) in the scope, click the
Scope tab on the spectrum analyzer toolstrip and navigate to
the Bandwidth section. You can enable this property in the status
bar at the bottom of the spectrum analyzer window. Click the ![]() icon in the status bar and select
icon in the status bar and select Sample
Rate.
Resolution bandwidth controls the spectral resolution of the displayed signal. The RBW value determines the spacing between frequencies that the scope can resolve. A smaller value gives a higher spectral resolution and lowers the noise floor, that is, the spectrum analyzer can resolve frequencies that are closer to each other. However, this comes at the cost of a longer sweep time.
You can specify the resolution bandwidth using the RBW (Hz) parameter.
If you specify the window length, the scope determines the RBW value from the window length using this equation, .
When you specify the Resolution
Method to RBW, and you set RBW
(Hz) to:
Auto–– The spectrum analyzer determines the appropriate resolution bandwidth to ensure that there are 1024 RBW intervals over the specified frequency span. When you set RBW (Hz) toAuto, the spectrum analyzer calculates using this equation.scalar value –– Specify a value such that there are at least two RBW intervals over the specified frequency span. The ratio of the overall span to RBW must be greater than two:
span is the frequency span over which the spectrum analyzer
computes and plots the spectrum. Spectrum analyzer shows the span through the
Span (Hz) property. To view the Span (Hz)
in the scope, click the Estimation tab on the spectrum analyzer
toolstrip, navigate to the Frequency Options section, and set
Frequency Span to Span and Center
Frequency.
When you specify the Resolution
Method to Number of frequency bands, the
resulting RBW is given by:
When the number of input samples is not sufficient to achieve the specified resolution bandwidth, the spectrum analyzer adjusts its RBW value according to the number of input samples provided and displays a message similar to this one. The spectrum analyzer removes this message once you provide enough input samples.

You can enable this property in the status bar at the bottom of the spectrum analyzer
window. Click the ![]() icon in the status bar and select
icon in the status bar and select
RBW.
When you plot the two-sided spectrum by selecting Two-Sided Spectrum in the Spectrum or Spectrogram tab, the Nyquist frequency interval is Hz.
When you clear the Two-Sided Spectrum, the Nyquist frequency interval is Hz.
When you set Frequency (Hz) to Auto, the software calculates the frequency vector for the frequency-domain input.
When you plot the two-sided spectrum by selecting Two-Sided Spectrum in the Spectrum or Spectrogram tab, the frequency vector is:
When you clear the Two-Sided Spectrum, the frequency vector is:
The spectrum analyzer calculates Occupied BW using these steps.
Calculate the total power in the measured frequency range.
Determine the lower frequency value. Starting at the lowest frequency in the range and moving upward, sum the power distributed in each frequency until the result is
of the total power.
Determine the upper frequency value. Starting at the highest frequency in the range and moving downward, sum the power distributed in each frequency until the result reaches
of the total power.
The bandwidth between the lower and upper power frequency values is the occupied bandwidth.
The frequency halfway between the lower and upper frequency values is the center frequency.
The spectrum analyzer calculates Distortion Measurements using these steps.
Estimate spectral content by finding peaks in the spectrum. When the algorithm detects a peak, it records the width of the peak and clears all monotonically decreasing values by treating all these values as if they belong to the peak. Using this method, the algorithm removes all spectral content centered at DC (0 Hz) from the spectrum and records the amount of bandwidth cleared (W0).
Determine the fundamental power (P1) from the remaining maximum value of the displayed spectrum. Create a local estimate (Fe1) of the fundamental frequency by computing the central moment of the power near the peak. Record the bandwidth of the fundamental power content (W1). Then remove the power from the fundamental as in step 1.
Determine the power and width of the higher-order harmonics (P2, W2, P3, W3, etc.) in succession by examining the frequencies closest to the appropriate multiple of the local estimate (Fe1). Remove any spectral content that decreases monotonically about the harmonic frequency from the spectrum before proceeding to the next harmonic.
After removing the DC, fundamental, and harmonic content from the spectrum, examine the power of the remaining spectrum for its sum (Premaining), peak value (Pmaxspur), and median value (Pestnoise).
Compute the sum of all the removed bandwidth as Wsum = W0 + W1 + W2 +...+ Wn.
Compute the sum of powers of the second and higher-order harmonics as Pharmonic = P2 + P3 + P4 +...+ Pn.
Estimate the sum of the noise power as:
Where dF is the absolute difference between frequency bins, and RBW is the resolution bandwidth of the window.
Then compute the metrics for THD, THD%, SINAD, SNR, and SFDR from the estimates.
The harmonic distortion measurements use the spectrum trace shown in the display as the input to the measurements. The default
Hannwindow setting of the spectrum analyzer might exhibit leakage that can completely mask the noise floor of the measured signal.The harmonic measurements attempt to correct for leakage by ignoring all frequency content that decreases monotonically away from the maximum of harmonic peaks. If the window leakage covers more than 70% of the frequency bandwidth in your spectrum, you may see a blank reading (–) reported for SNR and SINAD. If your application can tolerate the increased equivalent noise bandwidth (ENBW), consider using a Kaiser window with a high attenuation (up to 330 dB) to minimize spectral leakage.
Ignore the DC component.
After windowing, the width of each harmonic component masks the noise power in the neighborhood of the fundamental frequency and harmonics. To estimate the noise power in each region, the spectrum analyzer computes the median noise level in the nonharmonic areas of the spectrum. It then extrapolates that value into each region.
Nth order intermodulation products occur at A*F1 + B*F2,
where F1 and F2 are the sinusoid input frequencies and |A| + |B| = N. A and B are integer values.
For intermodulation measurements, compute the third-order intercept (TOI) point as follows.
TOIlower = PF1 + (PF2 - P(2F1-F2))/2
TOIupper = PF2 + (PF1 - P(2F2-F1))/2
TOI = + (TOIlower + TOIupper)/2
Where P is power in decibels of the measured power referenced to 1 milliwatt (dBm).
The spectrum analyzer calculates the moving average using one of these methods:
Video bandwidth — The spectrum analyzer uses a time-domain lowpass filter to smooth the noise in the signal. The video bandwidth (VBW) filter smoothes the trace and decreases noise, and the spectrum analyzer applies the filter to the data before displaying it.
Video bandwidth is the bandwidth of the lowpass filter that spectrum analyzer uses to average or smooth the noise in the signal before displaying it in the scope. The spectrum analyzer computes the video bandwidth using this equation:
where,
Video bandwidth does not affect the level of the noise (noise floor), but only increases the signal-to-noise ratio and smoothes the trace of the noise. When you decrease the value of VBW, the signal-to-noise ratio improves.
The cutoff frequency of the video bandwidth filter is given by:
where Fs is the input sample rate and NFFT is the number of FFT points.
The spectrum analyzer shows the values of sample rate, VBW, and NFFT in the status bar at the bottom of the display. To enable, right-click the status bar and select
Sample Rate,VBW, andNFFT.Exponential — The moving average algorithm uses the exponential weighting method to update the weights and compute the moving average recursively for each Z vector that comes in by using the following recursive equations:
λ — Forgetting factor
— Weighting factor applied to the current Z vector
— Current Z vector
— Moving average until the previous Z vector
— Effect of the previous Z vectors on the average
— Moving average including the current Z vector
Running –– For each frame of the input, average the last Q scaled Z vectors, which are computed by the algorithm. The variable Q is the value you specify for the number of spectral averages. If the algorithm does not have enough Z vectors, the algorithm uses zeros to fill the empty elements.
Extended Capabilities
Usage notes and limitations:
Supports MEX code generation by treating the calls to the object as extrinsic. Does not support code generation for standalone applications.
See System Objects in MATLAB Code Generation (MATLAB Coder).
Version History
Introduced in R2012bThe dsp.SpectrumAnalyzer
System object warns in R2024a. Use the spectrumAnalyzer
object instead.
Update Code
The spectrumAnalyzer object has the same properties as the
dsp.SpectrumAnalyzer object. However, the default value of the
Method property has changed to 'filter-bank', and
the default value of the AveragingMethod property has changed to
'vbw', which is video bandwidth.
No updates to your code are required except for:
Replacing instances of
dsp.SpectrumAnalyzerwithspectrumAnalyzer.Updating the values of
MethodandAveragingMethodproperties, if required.
This table shows how the System object is typically used and explains how to update existing code to use the
spectrumAnalyzer object.
| Discouraged Usage | Recommended Replacement |
|---|---|
Using the default version of
sa = dsp.SpectrumAnalyzer dsp.SpectrumAnalyzer with properties:
NumInputPorts: 1
InputDomain: 'time'
SpectrumType: 'power'
ViewType: 'spectrum'
SampleRate: 10000
Method: 'welch'
PlotAsTwoSidedSpectrum: 1
FrequencyScale: 'linear'
PlotType: 'line'
AxesScaling: 'auto'
Show all properties
| Replacing with the
The
To retain the same default
behavior as the sa = spectrumAnalyzer(Method="welch",... AveragingMethod="exponential") spectrumAnalyzer with properties:
InputDomain: 'time'
SpectrumType: 'power'
ViewType: 'spectrum'
SampleRate: 10000
Method: 'welch'
PlotAsTwoSidedSpectrum: 1
FrequencyScale: 'linear'
PlotType: 'line'
AxesScaling: 'auto'
Advanced
FrequencyResolutionMethod: 'rbw'
RBWSource: 'auto'
FFTLengthSource: 'auto'
FrequencySpan: 'full'
OverlapPercent: 0
Window: 'hann'
AveragingMethod: 'exponential'
ForgettingFactor: 0.9000
SpectrumUnits: 'dBm'
ReferenceLoad: 1
FrequencyOffset: 0
|
Display spectrum Display
spectrum data on the Spectrum Analyzer using the
swv = dsp.SineWave(Frequency=100,SampleRate=1000); swv.SamplesPerFrame = 1000; san = dsp.SpectrumAnalyzer(SampleRate=swv.SampleRate); data = []; for ii = 1:250 x = swv() + 0.05*randn(1000,1); san(x); if san.isNewDataReady data = [data;getSpectrumData(san)]; end end release(san); | Display spectrum Display
spectrum data on the Spectrum Analyzer using the swv = dsp.SineWave(Frequency=100,SampleRate=1000); swv.SamplesPerFrame = 1000; san = spectrumAnalyzer(SampleRate=swv.SampleRate,... Method="welch",AveragingMethod="exponential"); data = []; for ii = 1:250 x = swv() + 0.05*randn(1000,1); san(x); if san.isNewDataReady data = [data;getSpectrumData(san)]; end end release(san); |
The dsp.SpectrumAnalyzer
System object will be removed in a future release. Use the spectrumAnalyzer
object instead.
The CCDFMeasurements property will be removed from the dsp.SpectrumAnalyzer object. If you try to edit these measurements from the
command line or from the user interface (UI), the object throws a warning message.
Use the powermeter object
instead to plot and visualize the CCDF measurements.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)