Bootstrap Using Chain Ladder Method
This example shows how to apply a chain ladder bootstrap method to generate several developmentTriangle objects to estimate the ultimate claims.
Deterministic claim estimation methods produce point estimates of reserve values with no information about the uncertainty of these estimates. The goal of a stochastic claim estimation method is to assess the variability of estimated reserve values. The chain ladder bootstrapping approach is a simulation-based method to randomly modify the developmentTriangle data and produce a distribution of estimated reserves that represents the variability of the estimated reserve values. This example is based on the work of Wüthrich and Merz [1].
Load Data
load('InsuranceClaimsData.mat');
disp(head(data)); OriginYear DevelopmentYear ReportedClaims PaidClaims
__________ _______________ ______________ __________
2010 12 3995.7 1893.9
2010 24 4635 3371.2
2010 36 4866.8 4079.1
2010 48 4964.1 4487
2010 60 5013.7 4711.4
2010 72 5038.8 4805.6
2010 84 5059 4853.7
2010 96 5074.1 4877.9
Create developmentTriangle
Create a developmentTriangle object and use claimsPlot to visualize the developmentTriangle. For more information on unpaid claims estimation, see Overview of Claims Estimation Methods for Non-Life Insurance.
dTriangle = developmentTriangle(data);
dTriangleTable = view(dTriangle);
% visualize the development triangle
claimsPlot(dTriangle)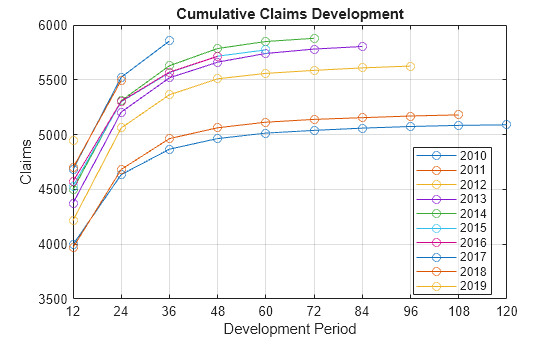
Analyze the developmentTriangle
The developmentTriangle link ratios are estimated using the formula:
Use linkRatios to calculate the age-to-age factors.
factorsTable = linkRatios(dTriangle);
Use linkRatioAverages to calculate the averages of the age-to-age factors.
averageFactorsTable = linkRatioAverages(dTriangle); disp(averageFactorsTable);
12-24 24-36 36-48 48-60 60-72 72-84 84-96 96-108 108-120
______ ______ ______ ______ ______ ______ _____ ______ _______
Simple Average 1.1767 1.0563 1.0249 1.0107 1.0054 1.0038 1.003 1.002 1.001
Simple Average - Latest 5 1.172 1.056 1.0268 1.0108 1.0054 1.0038 1.003 1.002 1.001
Simple Average - Latest 3 1.17 1.0533 1.027 1.0117 1.0057 1.0037 1.003 1.002 1.001
Medial Average - Latest 5x1 1.1733 1.0567 1.0267 1.0103 1.005 1.004 1.003 1.002 1.001
Volume-weighted Average 1.1766 1.0563 1.025 1.0107 1.0054 1.0038 1.003 1.002 1.001
Volume-weighted Average - Latest 5 1.172 1.056 1.0268 1.0108 1.0054 1.0038 1.003 1.002 1.001
Volume-weighted Average - Latest 3 1.1701 1.0534 1.027 1.0117 1.0057 1.0037 1.003 1.002 1.001
Geometric Average - Latest 4 1.17 1.055 1.0267 1.011 1.0055 1.0037 1.003 1.002 1.001
Display the selected age-to-age factors table and calculate the cumulative development factor (CDF) using cdfSummary.
dTriangle.SelectedLinkRatio = averageFactorsTable{'Volume-weighted Average',:};
currentSelectedFactors = dTriangle.SelectedLinkRatio;
dTriangle.TailFactor = 1;
selectedFactorsTable = cdfSummary(dTriangle);
disp(selectedFactorsTable); 12-24 24-36 36-48 48-60 60-72 72-84 84-96 96-108 108-120 Ultimate
_______ _______ _______ _______ _______ ______ _______ _______ _______ ________
Selected 1.1766 1.0563 1.025 1.0107 1.0054 1.0038 1.003 1.002 1.001 1
CDF to Ultimate 1.3072 1.111 1.0518 1.0261 1.0153 1.0098 1.006 1.003 1.001 1
Percent of Total Claims 0.76501 0.90008 0.95075 0.97453 0.98496 0.9903 0.99402 0.99701 0.999 1
Display the latest diagonal.
latestDiagonal = dTriangle.LatestDiagonal;
Compute the projected ultimate claims using ultimateClaims.
projectedUltimateClaims = ultimateClaims(dTriangle);
Display the full development triangle using fullTriangle.
fullTriangleTable = fullTriangle(dTriangle); disp(fullTriangleTable);
12 24 36 48 60 72 84 96 108 120 Ultimate
______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ________
2010 3995.7 4635 4866.8 4964.1 5013.7 5038.8 5059 5074.1 5084.3 5089.4 5089.4
2011 3968 4682.3 4963.2 5062.5 5113.1 5138.7 5154.1 5169.6 5179.9 5185.1 5185.1
2012 4217 5060.4 5364 5508.9 5558.4 5586.2 5608.6 5625.4 5636.7 5642.3 5642.3
2013 4374.2 5205.3 5517.7 5661.1 5740.4 5780.6 5803.7 5821.1 5832.7 5838.6 5838.6
2014 4499.7 5309.6 5628.2 5785.8 5849.4 5878.7 5900.8 5918.5 5930.3 5936.3 5936.3
2015 4530.2 5300.4 5565.4 5715.7 5772.8 5804.1 5825.9 5843.4 5855.1 5861 5861
2016 4572.6 5304.2 5569.5 5714.3 5775.4 5806.7 5828.6 5846.1 5857.7 5863.6 5863.6
2017 4680.6 5523.1 5854.4 6000.9 6065.1 6098 6120.9 6139.3 6151.6 6157.7 6157.7
2018 4696.7 5495.1 5804.4 5949.6 6013.3 6045.9 6068.6 6086.8 6099 6105.1 6105.1
2019 4945.9 5819.2 6146.7 6300.5 6367.9 6402.4 6426.5 6445.8 6458.7 6465.2 6465.2
Compute the total reserves using ultimateClaims.
IBNR = ultimateClaims(dTriangle) - dTriangle.LatestDiagonal; IBNR = array2table(IBNR, 'RowNames', dTriangleTable.Properties.RowNames, 'VariableNames', {'IBNR'}); IBNR{'Total',1} = sum(IBNR{:,:}); disp(IBNR);
IBNR
______
2010 0
2011 5.1857
2012 16.89
2013 34.886
2014 57.583
2015 88.148
2016 149.34
2017 303.29
2018 609.99
2019 1519.3
Total 2784.6
Bootstrap Chain Ladder
To derive the resampling approaches, the Time Series Model of the distribution-free chain ladder (CL) model is defined as:
For the link ratio selected above, Wüthrich [1] and Mack [2] show that the standard deviation is estimated as:
estimatedStandardDeviations = currentSelectedFactors; for i=1:width(estimatedStandardDeviations)-1 estimatedStandardDeviations(1,i) = sqrt(sum(((factorsTable{1:end-i,i} - currentSelectedFactors(:,i)).^2).*dTriangleTable{1:end-i,i}) / (height(dTriangleTable)-i-1)); end estimatedStandardDeviations(1,end) = sqrt(min([estimatedStandardDeviations(1,end-1)^4 / estimatedStandardDeviations(1,end-2)^2, estimatedStandardDeviations(1,end-2)^2, estimatedStandardDeviations(1,end-1)^2])); disp(estimatedStandardDeviations);
0.8667 0.3699 0.2420 0.1310 0.0673 0.0361 0.0001 0.0001 0.0001
To apply the bootstrap method, you need to find the appropriate residuals that allow for the construction of the empirical distribution to construct the bootstrap observations.
Consider the following residuals for .
where
Following Wüthrich [1], you can scale the residuals to adjust their variance upwards. Unscaled residuals tend to result in lighter tails in the simulated distribution.
Adjust the residuals such that the bootstrap distribution has an adjusted variance function.
You can apply the bootstrap algorithm using three different versions:
Efron's nonparametric bootstrap for residuals
Efron's nonparametric bootstrap for scaled residuals
Parametric bootstrap under the assumption that the residuals have a standard Gaussian distribution, that is is resampled from
This example uses the second version (Efron's nonparametric bootstrap for scaled residuals) to calculate .
% Create a copy of the factors table and modify it to create the % residuals table residuals = factorsTable.Variables; colSums = sum(dTriangle.Claims,'omitnan'); for i=1:height(residuals) for j=1:width(residuals) residuals(i,j) = (1 - (dTriangleTable{i,j}/colSums(j)))^-0.5 * (factorsTable{i,j} - currentSelectedFactors(1,j)) / (estimatedStandardDeviations(1,j)*(dTriangleTable{i,j}^-0.5)); end end
The residuals define a bootstrap distribution.
residualsVector = residuals(:); residualsVector(isnan(residualsVector)) = []; histogram(residualsVector,10) title('Scaled Residuals') xlabel('Residual Value') ylabel('Frequency')

To simulate a new reserves scenario with the bootstrap method, follow these steps.
Step 1: Resample a triangle of residuals from the bootstrap distribution.
Resample the independent and identically distributed (i.i.d.) residuals from the bootstrap distribution.
resampledResiduals = residuals; rng('default'); rng(1); for i = 1:height(residuals)-1 for j = 1:width(residuals)-i+1 resampledResiduals(i,j) = datasample(residuals(~isnan(residuals)), 1); end end disp(resampledResiduals);
-1.5522 -0.5120 -1.2668 0.7776 -1.3649 0.2799 -0.5495 -1.3146 -1.5364
-0.4041 -1.5522 -0.4784 -1.2189 -0.7591 0.2610 -0.4784 -1.5522 NaN
-0.4091 -1.3649 -0.5495 -1.6767 -0.8571 -1.3143 -0.4879 NaN NaN
-0.7591 1.3226 1.0791 0.2610 0.2861 -0.7591 NaN NaN NaN
0.2799 -1.5522 -0.8571 0.3243 -0.4879 NaN NaN NaN NaN
-1.3143 -0.4784 0.5556 -1.2668 NaN NaN NaN NaN NaN
1.9550 0 1.9550 NaN NaN NaN NaN NaN NaN
0.7693 0.5169 NaN NaN NaN NaN NaN NaN NaN
0.2799 NaN NaN NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN NaN NaN NaN
Step 2: Compute bootstrapped claims.
Define and, for , assume that:
This expression represents the new simulated claim values. Using the simulated claim values, you can create a new developmentTriangle to estimate new reserve values.
bootstrappedClaims = dTriangleTable.Variables; for j = 2:width(bootstrappedClaims) bootstrappedClaims(:,j) = currentSelectedFactors(1,j-1).*bootstrappedClaims(:,j-1) + estimatedStandardDeviations(1,j-1).*sqrt(bootstrappedClaims(:,j-1)).*resampledResiduals(:,j-1); end stackedClaims = reshape(bootstrappedClaims',100,1); stackedClaims = stackedClaims(~isnan(stackedClaims)); newData = data; newData.values = stackedClaims; bootstrappedDevelopmentTriangle = developmentTriangle(newData,'Claims','values');
Step 3: Select a link ratio consistent with the model.
The volume-weighted average is the link ratio that is consistent with the model used in this bootstrap approach.
bootstrappedAverageFactorsTable = linkRatioAverages(bootstrappedDevelopmentTriangle);
bootstrappedDevelopmentTriangle.SelectedLinkRatio = bootstrappedAverageFactorsTable{'Volume-weighted Average',:};
bootstrappedDevelopmentTriangle.TailFactor = 1;
bootstrappedSelectedFactorsTable = cdfSummary(bootstrappedDevelopmentTriangle);
disp(bootstrappedSelectedFactorsTable); 12-24 24-36 36-48 48-60 60-72 72-84 84-96 96-108 108-120 Ultimate
_______ _______ ______ _______ _______ ______ _______ _______ _______ ________
Selected 1.1751 1.054 1.0253 1.0099 1.0048 1.0036 1.003 1.002 1.001 1
CDF to Ultimate 1.301 1.1072 1.0504 1.0245 1.0145 1.0096 1.006 1.003 1.001 1
Percent of Total Claims 0.76861 0.90321 0.952 0.97609 0.98572 0.9905 0.99403 0.99701 0.999 1
Use fullTriangle to display the full development triangle corresponding to the selected link ratio.
bootstrappedFullTriangle = fullTriangle(bootstrappedDevelopmentTriangle); disp(bootstrappedFullTriangle);
12 24 36 48 60 72 84 96 108 120 Ultimate
______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ________
2010 3995.7 4616.2 4863.2 4963.4 5023.7 5044.5 5064.1 5079.3 5089.5 5094.6 5094.6
2011 3968 4646.6 4869 4982.8 5024.8 5048.4 5068.1 5083.3 5093.4 5098.5 5098.5
2012 4217 4938.6 5181.1 5301.1 5341.9 5366.6 5383.3 5399.5 5410.2 5415.6 5415.6
2013 4374.2 5103.1 5425.3 5580.2 5642.5 5674.5 5693.8 5710.9 5722.3 5728 5728
2014 4499.7 5310.5 5567.5 5691.3 5755.4 5784.2 5804.8 5822.2 5833.8 5839.6 5839.6
2015 4530.2 5253.5 5536.3 5684.8 5733.2 5761 5781.5 5798.8 5810.4 5816.2 5816.2
2016 4572.6 5494.6 5803.9 5985.1 6044.2 6073.5 6095.1 6113.4 6125.6 6131.7 6131.7
2017 4680.6 5552.6 5879.4 6028.2 6087.7 6117.2 6139 6157.4 6169.7 6175.9 6175.9
2018 4696.7 5542.6 5842 5989.8 6048.9 6078.2 6099.9 6118.2 6130.4 6136.5 6136.5
2019 4945.9 5812 6126 6281 6343 6373.7 6396.4 6415.6 6428.4 6434.8 6434.8
Step 4: Compute the total reserves.
Compute the total reserves from the simulated developmentTriangle.
bootstrappedDevelopmentTriangleTable = view(bootstrappedDevelopmentTriangle); bootstrappedIBNR = ultimateClaims(bootstrappedDevelopmentTriangle) - bootstrappedDevelopmentTriangle.LatestDiagonal; bootstrappedIBNR = array2table(bootstrappedIBNR, 'RowNames', bootstrappedDevelopmentTriangleTable.Properties.RowNames, 'VariableNames', {'IBNR'}); bootstrappedIBNR{'Total',1} = sum(bootstrappedIBNR{:,:}); disp(bootstrappedIBNR);
IBNR
______
2010 0
2011 5.0881
2012 16.188
2013 34.197
2014 55.485
2015 83.048
2016 146.61
2017 296.45
2018 593.94
2019 1489
Total 2720
You can repeat the previous steps many times to generate a full, simulated, distribution of reserves. The simulation produces reserves for each year and for the total reserves.
Simulate Multiple Bootstrapped Scenarios
Create 1000 bootstrapped development triangles and calculate the incurred-but-not-reported (IBNR) for each developmentTriangle.
n = 1000; simulatedIBNR = zeros(10,n); for i = 1:n simulatedResiduals = residuals; for j = 1:height(residuals)-1 for k = 1:width(residuals)-j+1 simulatedResiduals(j,k) = datasample(residuals(~isnan(residuals)),1); end end simulatedClaims = dTriangleTable.Variables; for j = 2:width(simulatedClaims) simulatedClaims(:,j) = currentSelectedFactors(1,j-1).*simulatedClaims(:,j-1) + estimatedStandardDeviations(1,j-1).*sqrt(simulatedClaims(:,j-1)).*simulatedResiduals(:,j-1); end simulatedClaims = reshape(simulatedClaims',100,1); simulatedClaims = simulatedClaims(~isnan(simulatedClaims)); simulatedData = data; simulatedData.ReportedClaims = simulatedClaims; simulatedDevelopmentTriangle = developmentTriangle(simulatedData); simulatedAverageFactorsTable = linkRatioAverages(simulatedDevelopmentTriangle); simulatedDevelopmentTriangle.SelectedLinkRatio = simulatedAverageFactorsTable{'Volume-weighted Average',:}; simulatedDevelopmentTriangle.TailFactor = 1; simulatedLatestDiagonal = simulatedDevelopmentTriangle.LatestDiagonal; simulatedProjectedUltimateClaims = ultimateClaims(simulatedDevelopmentTriangle); simulatedIBNR(:,i) = simulatedProjectedUltimateClaims - simulatedLatestDiagonal; end simulatedIBNR(end+1,:) = sum(simulatedIBNR);
Select a year to plot the distribution of the IBNR, calculate the mean, and compare that mean to a calculated deterministic value.
originYear =5; histogram(simulatedIBNR(originYear+1,:)); hold on; plot(mean(simulatedIBNR(originYear+1,:)),0,'O','LineWidth',2) plot(IBNR{originYear+1,1},0,'X','LineWidth',2); legend('Simulated IBNR',['Simulated mean : ' num2str(round(mean(simulatedIBNR(originYear+1,:)),2))],['Deterministic IBNR : ' num2str(round(IBNR{originYear+1,1},2))]); hold off;
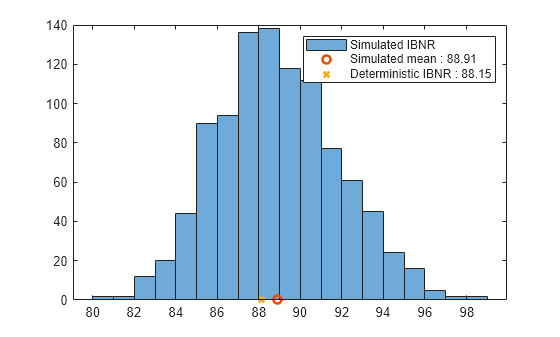
Plot a histogram of the totals for IBNRs, simulated means, and deterministic values.
histogram(simulatedIBNR(11,:)); hold on; plot(mean(simulatedIBNR(11,:)),0,'O','LineWidth',2) plot(IBNR{11,1},0,'X','LineWidth',2); legend('Simulated Total IBNR',['Simulated mean : ' num2str(round(mean(simulatedIBNR(11,:)),2))],['Deterministic Total IBNR : ' num2str(round(IBNR{11,1},2))]); hold off;
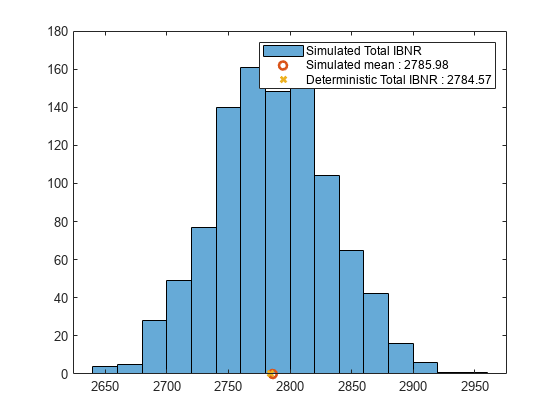
References
Wüthrich, Mario, and Michael Merz. Stochastic Claims Reserving Methods in Insurance. Hoboken, NJ: Wiley, 2008
Mack, Thomas. "Distribution-Free Calculation of the Standard Error of Chain Ladder Reserve Estimates." Astin Bulletin. Vol. 23, No. 2, 1993.
See Also
developmentTriangle | view | linkRatios | linkRatiosPlot | linkRatioAverages | cdfSummary | ultimateClaims | claimsPlot | fullTriangle | chainLadder | expectedClaims | bornhuetterFerguson | capeCod