systune
Tune control system parameters in Simulink using slTuner interface
Syntax
Description
systune tunes fixed-structure control systems subject to both
soft and hard design goals. systune can tune multiple fixed-order,
fixed-structure control elements distributed over one or more feedback loops. For an overview
of the tuning workflow, see Automated Tuning Workflow.
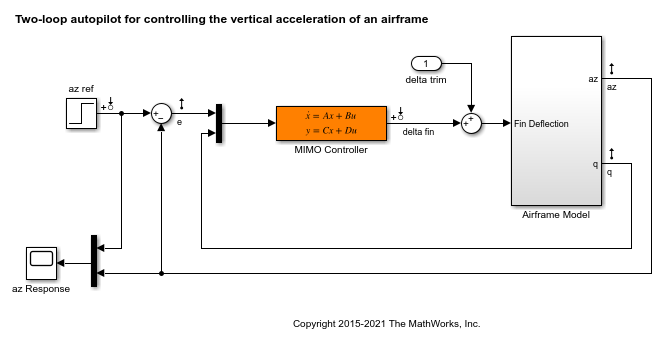
This command tunes control systems modeled in Simulink®. For tuning control systems represented in MATLAB®, use systune for genss models.
[ tunes
the free parameters of the control system in Simulink. The Simulink model, tuned blocks, and analysis points of
interest are specified by the st,fSoft]
= systune(st0,SoftGoals)slTuner interface, st0. systune tunes
the control system parameters to best meet the performance goals, SoftGoals.
The command returns a tuned version of st0 as st.
The best achieved soft constraint values are returned as fSoft.
If the st0 contains real parameter uncertainty, systune automatically
performs robust tuning to optimize the constraint values for worst-case
parameter values. systune also performs robust
tuning against a set of plant models obtained at different operating
points or parameter values. See Input Arguments.
Tuning is performed at the sample time specified by the Ts property
of st0.
Examples
Input Arguments
Output Arguments
More About
Algorithms
x is the vector of tunable parameters in
the control system to tune. systune converts each
soft and hard tuning requirement SoftReqs(i) and HardReqs(j) into
normalized values fi(x)
and gj(x),
respectively. systune then solves the constrained
minimization problem:
Minimize subject to , for .
xmin and xmax are the minimum and maximum values of the free parameters of the control system.
When you use both soft and hard tuning goals, the software approaches this optimization problem by solving a sequence of unconstrained subproblems of the form:
The software adjusts the multiplier α so that the solution of the subproblems converges to the solution of the original constrained optimization problem.
systune returns the slTuner interface with parameters tuned
to the values that best solve the minimization problem. systune also
returns the best achieved values of fi(x)
and gj(x),
as fSoft and gHard respectively.
For information about the functions fi(x)
and gj(x)
for each type of constraint, see the reference pages for each TuningGoal requirement
object.
systune uses the nonsmooth optimization algorithms
described in [1],[2],[3],[4]
systune computes the H∞
norm using the algorithm of [5] and structure-preserving eigensolvers from the SLICOT library. For information about the
SLICOT library, see https://github.com/SLICOT.
Alternative Functionality
Tune interactively using Control System Tuner.
References
[1] P. Apkarian and D. Noll, "Nonsmooth H-infinity Synthesis," IEEE Transactions on Automatic Control, Vol. 51, Number 1, 2006, pp. 71–86.
[2] Apkarian, P. and D. Noll, "Nonsmooth Optimization for Multiband Frequency-Domain Control Design," Automatica, 43 (2007), pp. 724–731.
[3] Apkarian, P., P. Gahinet, and C. Buhr, "Multi-model, multi-objective tuning of fixed-structure controllers," Proceedings ECC (2014), pp. 856–861.
[4] Apkarian, P., M.-N. Dao, and D. Noll, "Parametric Robust Structured Control Design," IEEE Transactions on Automatic Control, 2015.
[5] Bruinsma, N.A., and M. Steinbuch. "A Fast Algorithm to Compute the H∞ Norm of a Transfer Function Matrix." Systems & Control Letters, 14, no.4 (April 1990): 287–93.
Extended Capabilities
Version History
Introduced in R2014a
See Also
systune (for
genss) | systuneOptions | slTuner | addPoint | getIOTransfer | getLoopTransfer | writeBlockValue | looptune | hinfstruct (Robust Control Toolbox)