Transforms
Fourier, chirp Z, DCT, Hilbert, cepstrum, Walsh-Hadamard
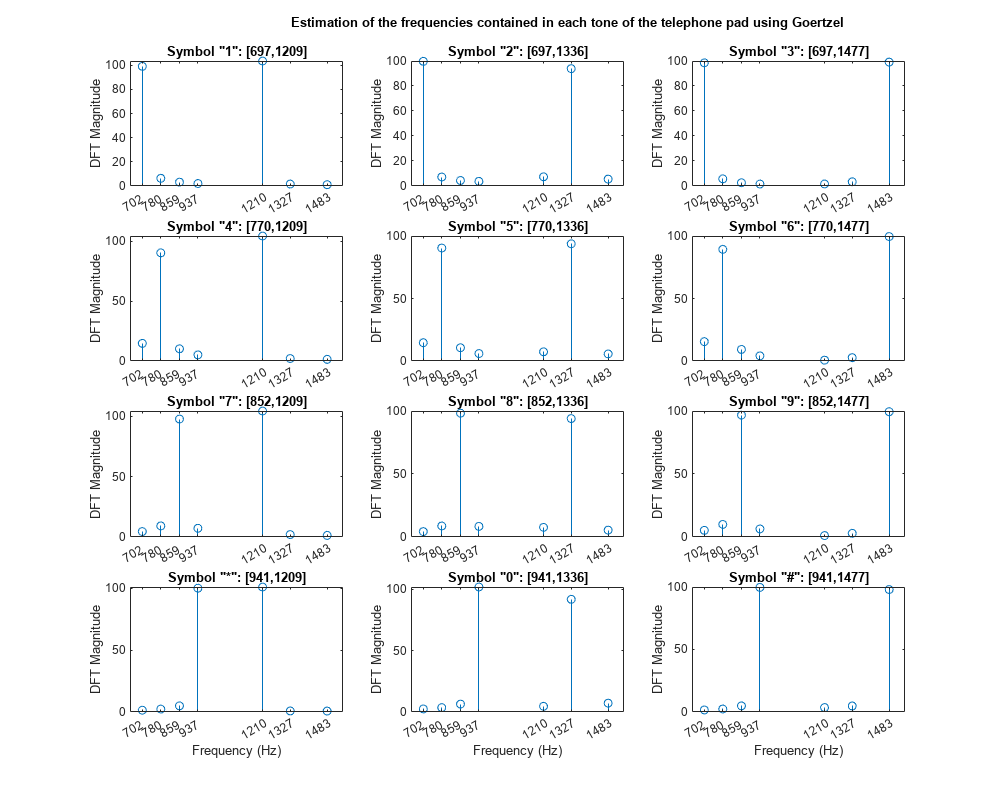
Signal Processing Toolbox™ provides functions that let you compute widely used forward and inverse transforms, including the fast Fourier transform (FFT), the discrete cosine transform (DCT), and the Walsh-Hadamard transform. Extract signal envelopes and estimate instantaneous frequencies using the analytic signal. Analyze signals in the time-frequency domain. Investigate magnitude-phase relationships, estimate fundamental frequencies, and detect spectral periodicity using the cepstrum. Compute discrete Fourier transforms using the second-order Goertzel algorithm.
Functions
Topics
Discrete Fourier and Cosine Transforms
- Discrete Fourier Transform
Explore the primary tool of digital signal processing. - Chirp Z-Transform
Use the CZT to evaluate the Z-transform outside of the unit circle and to compute transforms of prime length. - Discrete Cosine Transform
Compute discrete cosine transforms and learn about their energy compaction properties. - DCT for Speech Signal Compression
Use the discrete cosine transform to compress speech signals.
Hilbert and Walsh-Hadamard Transforms
- Hilbert Transform
The Hilbert transform helps form the analytic signal. - Analytic Signal for Cosine
Determine the analytic signal for a cosine and verify its properties. - Envelope Extraction
Extract the envelope of a signal using thehilbertandenvelopefunctions. - Analytic Signal and Hilbert Transform
Generate the analytic signal for a finite block of data using thehilbertfunction and an FIR Hilbert transformer. - Hilbert Transform and Instantaneous Frequency
Estimate the instantaneous frequency of a monocomponent signal using the Hilbert transform. Show that the procedure does not work for multicomponent signals. - Single-Sideband Amplitude Modulation
Perform single-sideband amplitude modulation of a signal using the Hilbert transform. Single-sideband AM signals have less bandwidth than normal AM signals. - Walsh-Hadamard Transform
Learn about the Walsh-Hadamard transform, a non-sinusoidal, orthogonal transformation technique. - Walsh-Hadamard Transform for Spectral Analysis and Compression of ECG Signals
Use an electrocardiogram signal to illustrate the Walsh-Hadamard transform.
Cepstral Analysis
- Complex Cepstrum — Fundamental Frequency Estimation
Use the complex cepstrum to estimate a speaker’s fundamental frequency. Compare the result with the estimate obtained with a zero-crossing method. - Cepstrum Analysis
Apply the complex cepstrum to detect echo in a signal.